
Después de ver las funciones afines, cuadráticas y cubicas, ahora podemos estudiar funciones polinómicas de mayor grado.
Un modo interesante de general funciones polinómicas es usar los polinomios de interpolación de Lagrange. Dados n puntos en el plano, el polinomio de interpolación de Lagrange es el polinomio de grado igual (o menor) que (n-1) que pasa por esos n puntos.

Nuestro propósito es repasar algunos conceptos ya vistos y comprender mejor el comportamiento de diferentes funciones polinómicas y sus derivadas.
EL CONCEPTO DE DERIVADA DE UNA FUNCIÓN
La derivada de una función en un punto puede definirse como la tasa de variación instantánea o como la pendiente de la recta tangente a la gráfica de la función en ese punto. Podemos definir la pendiente de la función en un punto como la pendiente de la recta tangente.
La pendiente de la tangente depende, en general, de x. Entonces, a partir de una función podemos definir una nueva función, la función derivada de la función original.
El proceso de encontrar la función derivada de una función se llama diferenciación.
El valor de la función dericada para cada valor de x es la pendiente de la función original en x.
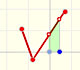
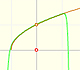
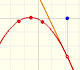
Una idea que ya hemos visto es la interpretación geométrica de la derivada como la pendiente de la recta tangente en cada punto:
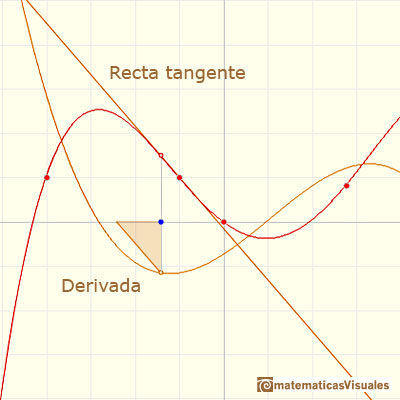
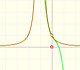
Pero, ¿cómo podemos dibujar la tangente? Podemos usar una lupa.
Si miramos muy cerca el punto en la gráfica de la función podemos ver cómo la recta tangente es muy semejante a la función. La recta tangente es la mejor aproximación lineal de la función en ese punto:
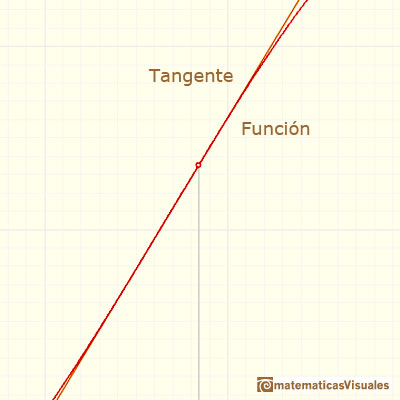
Esta idea es interesante e intuitiva pero, en la práctica, no sabemos dibujar con precisión una recta tangente 'a ojo'. La herramienta adecuada es la derivada.
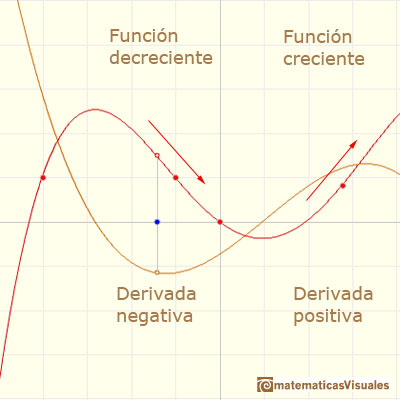
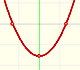
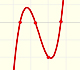
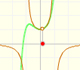
Ya hemos visto que las funciones polinómicas pueden tener 'zonas' (valores de x, intervalos de valores) para los que la función crece y otras zonas en las que decrece. Vemos este comportamiento en la gráfica con las 'subidas' y 'bajadas'.
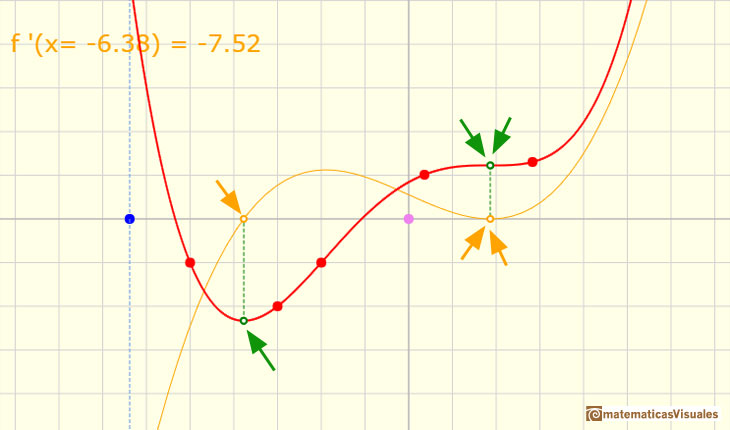
Hay una relación entre la derivada y el caracter creciente o decreciente de una función polinómica. Si la derivada es positiva en algún intervalo entonces la función es creciente en ese intervalo y si la derivada es negativa en algún intervalo entonces la función es decreciente en ese intervalo:
INVESTIGA
El número máximo de 'subidas' y 'bajadas' de una función polinómica, es decir, de intervalos de crecimiento y decremiento, está relacionado con el grado de esa función pues está determinado por el signo de su derivada.
Por ejemplo, un polinomio de grado 4 tiene una derivada de grado 3. Un polinomio de grado 3 (una función cúbica) tiene, por lo menos, un intervalo donde es positiva y otro donde es negativa. Podemos decir que, por lo menos, una función de grado 4 tendrá un intervalo de crecimiento y otro de decrecimiento. Pero no puede tener más de dos intervalos de crecimiento y dos de decrecimiento.
¿Sabrías justificar esta afirmación?
Estudia las diferentes posibilidades para polinomios de grado 4 y de grado 5.
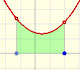
Si una función cambia de creciente a decreciente algún punto es 'la cima de la montaña' y lo llamamos MÁXIMO local o relativo. El 'fondo del valle' recibe el nombre de MÍNIMO local o relativo. En ambos casos hablamos de EXTREMOS locales o relativos de una función.
Es muy difícil determinar el valor exacto de esos máximo o mínimos solo mirando la gráfica de la función. Eso es debido a que la función varía muy poco alrededor de ese valor extremo.
Para calcular esos máximos y mínimos locales nos va a ser muy útil la derivada pues en esos valores la derivada se anula, vale 0.
Por lo tanto, si queremos encontrar los máximos y mínimos locales los tenemos que buscar entre aquellos en los que la derivada se anula.
Un punto ESTACIONARIO es un punto en el que la derivada se hace cero (la pendiente de la tangente es cero, la tangente es una recta horizontal). En esos puntos la función deja de crecer o decrecer. En el caso de las funciones polinómicas los puntos estacionarios son los mismos que los puntos CRÍTICOS (En general, los puntos críticos también incluyen aquellos puntos en los que la función no es derivable, esto no ocurre en el caso de las funciones polinómicas que son siempre derivables.).
En un punto estacionario la función puede cambiar de creciente a decreciente. Entonces ese punto estacionario es un máximo local (o máximo relativo). La derivada cambia de positiva a negativa.
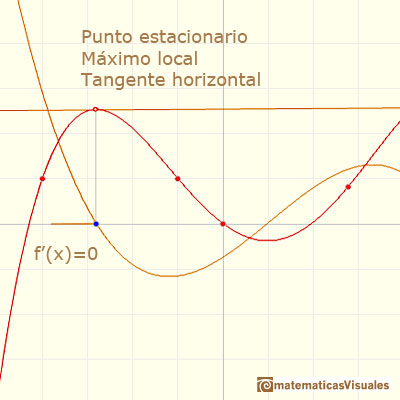
En otros casos, en un punto estacionario la función puede cambiar de decreciente a creciente. Entonces el punto estacionario es un mínimo local (o mínimo relativo). La derivada cambia de negativa a positiva.
Hay puntos estacionarios que no son máximos ni mínimos. Son puntos e inflexión, es decir, puntos en los que cambia el signo de la curvatura.
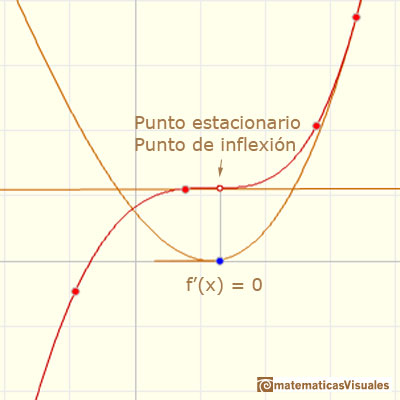
De los puntos de inflexión volveremos a hablar más adelante.
En resumen, para encontrar los puntos estacionarios tenemos que resolver una ecuación polinómica. Esto no es fácil en general pues tenemos dificultades para resolver ecuaciones de grado mayor que 2.
Lo que nos interesa destacar aquí es esta relación entre los ceros de la derivada y los candidatos a ser máximos y mínimos de la función.
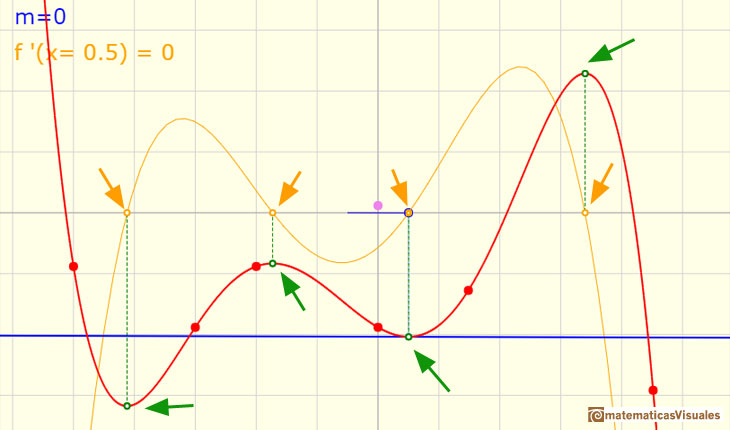
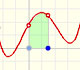
Los puntos de inflexión están relacionados con los máximos o mínimos locales de la función derivada. En estos puntos la tangente corta a la curva, la cruza.
INVESTIGA
En la aplicación interactiva no se muestran los puntos de inflexión de las funciones pero se puede ver cómo los puntos en los que la curvatura de la función cambia se corresponden con los máximos o mínimos de su derivada.
Prueba con diferentes funciones polinómicas y observa esta correspondencia.
Nos vamos a fijar ahora en un tipo particular de punto de inflexión. Si modificamos la función (moviendo los puntos rojos) veremos que los máximos y mínimos cambian, se aproximan o se alejan entre sí.
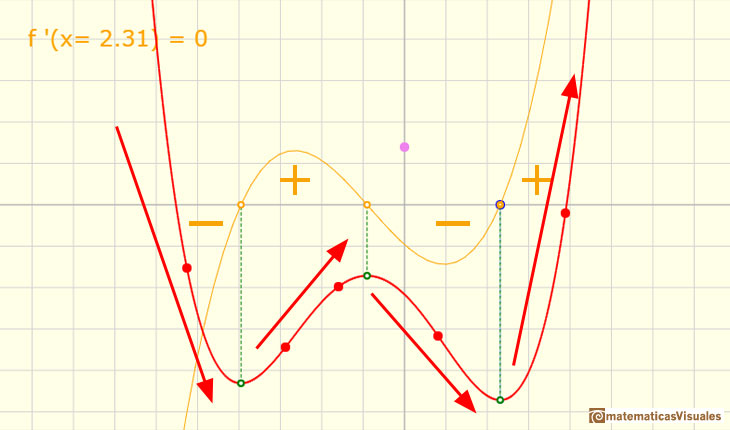
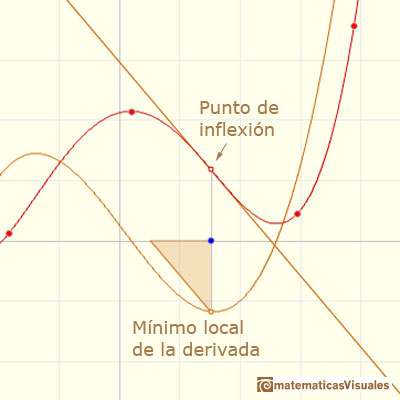
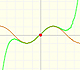
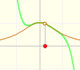
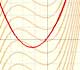
Podemos conseguir una situación semejante a la siguiente imagen que representa una función de grado 4 y su derivada. Dos ceros de la función derivada se han confundido en uno solo (un cero doble) y un máximo y un mínimo se han confundido en uno solo. Ya no son máximo y mínimo sino que es un punto de inflexión. Si nos fijamos en la derivada, en ese punto tenemos un cero y un mínimo.
La función de grado 4 tiene, por tanto, un mínimo local, un punto de inflexión que se corresponde con el máximo de la derivada (que no está marcado en el dibujo) y un punto de inflexión 'especial' que se corresponde con un mínimo de la derivada que, a la vez, es un cero.
INVESTIGA
Intenta reproducir puntos de inflexión de este tipo con diferentes funciones polinómicas.
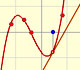
Una idea simple e interesante es que cuando trasladamos arriba y abajo el gráfico de la función (sumamos o restamos un número a la función original) la función derivada no cambia. La razón es muy intuitiva y podemos jugar con la siguiente versión del mathlet para ver esta propiedad. Cuando movemos el punto violeta trasladamos verticalmente la función y la función derivada no cambia:
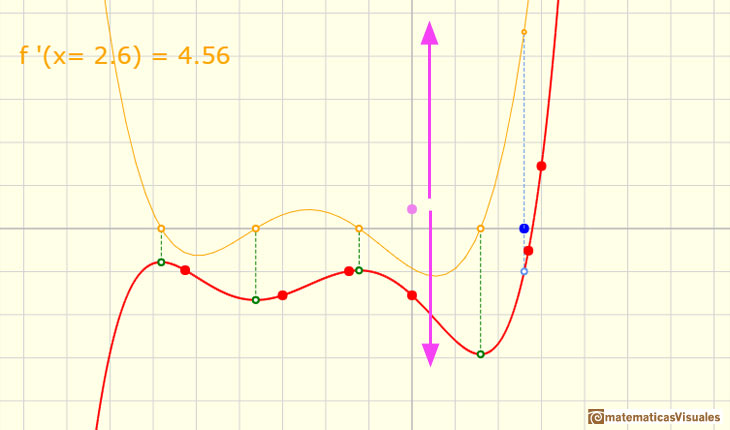
Es importante notar que la derivada de un polinomio de grado 1 es una función constante (un polinomio de grado 0). La derivada de un polinomio de grado 2 es un polinomio de grado 1. Y que la derivada de un polinomio de grado 3 es un polinomio de grado 2.
Cuando derivamos esas funciones polinómicas el resultado es un polinomio de un grado menor que la función original.
Cuando estudiamos la integral de un polinomio de grado 2 veremos que en este caso la nueva función es un polinomio de grado 3. Un grado más que la función original.
Estos resultados están relacionados con el Teorema Fundamental del Cálculo.
REFERENCIAS
 SIGUIENTE
SIGUIENTE
MÁS ENLACES


























 ANTERIOR
ANTERIOR
