Siguiendo a Tristan Needham, vamos a estudiar dos funciones racionales más para poder comprender mejor la convergencia de las series de potencias, lo que él llama "El misterio de las series de potencias reales".

Sabemos que muchas funciones reales F(x) pueden expresarse (por ejemplo, usando el Teorema de Taylor) como una serie de potencias, y que estas series infinitas normalmente convergen a F(x) sólamente en algún intervalo de convergencia -R < x < R. Pero ¿cómo R (el radio de convergencia) está determinado por F(x)?

Needham escribió: "Resulta que esta pregunta tiene una respuesta simple muy bonita, pero solo si la investigamos en el plano complejo. Si nos restringimos a la recta real -como estuvieron obligados los matemáticos en la era en la que estas series fueron utilizadas por primera vez- la relación entre R y F(x) es misteriosa. Históricamente, fue precisamente este misterio el que llevó a Cauchy a varios de sus avances en análisis complejo." (Tristan Needham, Visual Complex Analysis, p. 64)

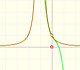
Consideramos ahora la función racional

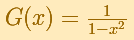
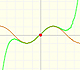
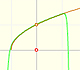
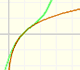
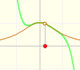
Su serie de potencias, centrada en el origen, tiene el intervalo de convergencia (-1, 1).

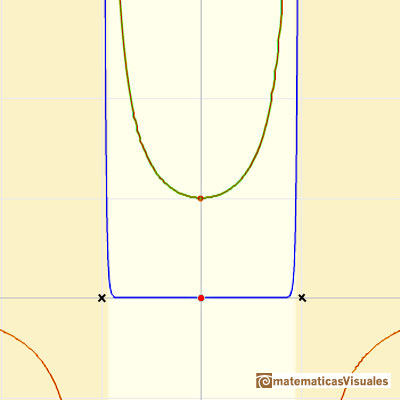
Nos resulta fácil entender que éste sea el intervalo de convergencia de la serie debido a que los puntos x = 1 and x = -1 son singularidades de la función. Son puntos en los que el módulo de la función se hace infinito.

Este comportamiento es similiar al de otras funciones con singularidades.

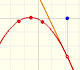
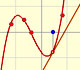
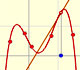
En el applet podemos cambiar el centro de la serie de potencias y podemos ver cómo el radio del intervalo de convergencia es la distancia desde el centro de la serie a la singularidad más próxima. Las singularidades actúan como barreras.

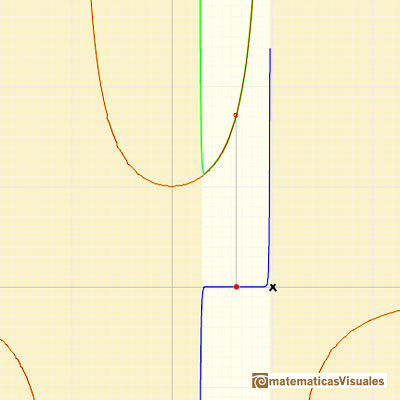
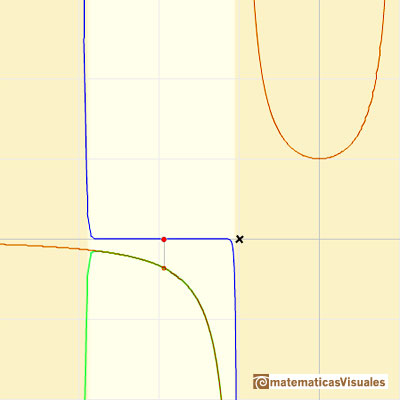
Podemos comparar este comportamiento con el de otra función que tiene un comportamiento más misterioso Polinomios de Taylor (7): función racional sin singularidades reales.

REFERENCIAS

MÁS ENLACES

Polinomios de Taylor: función racional compleja con 2 singularidades

Podemos estudiar la aproximación a esta función por el polinomio de Taylor y su convergencia en el círculo de convergencia.

Polinomios de Taylor (1): función exponencial

Al aumentar el grado del polinomio de Taylor se aproxima a la función exponencial en un intervalo más y más amplio.

Polinomios de Taylor (2): función seno

Al aumentar el grado del polinomio de Taylor se aproxima a la función seno en un intervalo más y más amplio.

Polinomios de Taylor (3): raíz cuadrada

La función no está definida para valores menores que -1. Los polinomios de Taylor en torno al origen aproximan la función entre -1 y 1.

Polinomios de Taylor (4): función racional 1

La función tiene una singularidad en -1. Los polinomios de Taylor en torno al origen aproximan la función entre -1 y 1.

Mercator y Euler: La función logaritmo

Mercator publicó su famosa serie para la función logaritmo en 1668. Euler descubrió una serie práctica para el cálculo.

Funciones polinómicas y derivada (1): Funciones afines

La derivada de una función lineal es la función constante cuyo valor es la pendiente de la recta.

Funciones polinómicas y derivada (2): Funciones cuadráticas

La derivada de una función cuadrática es una función afín, es decir, es una línea recta.

Funciones polinómicas y derivada (3): Funciones cúbicas

La derivada de una función cúbica es una función cuadráticas, es decir, una parábola

Funciones polinómicas y derivada (4): Polinomios de Lagrange (funciones polinómicas en general)

Los polinomios de Lagrange son polinomios que pasan por n puntos dados. Usamos los polinomios de Lagrange para explorar funciones polinómicas más generales y sus derivadas.