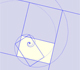
Partimos de un pentágono regular y queremos conocer la razón entre la diagonal y el lado de ese pentágono.
Podemos considerar que el lado del pentágono es 1. Entonces la diagonal se representa por
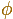, la letra griega phi.
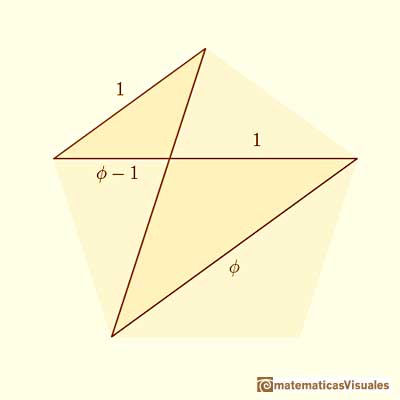
Nos fijamos en dos triángulos isósceles homotéticos:
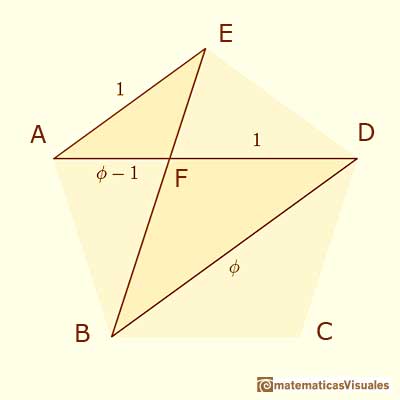
Podemos escribir la proporción:
Usando los números 1 y :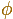
Entonces 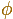es la raíz positiva de la ecuación cuadrática:
Resolviendo esta ecuación obtenemos el valor de :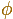
Estas son algunas propiedades de :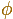
A 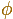se le llama la razón o proporción aúrea.
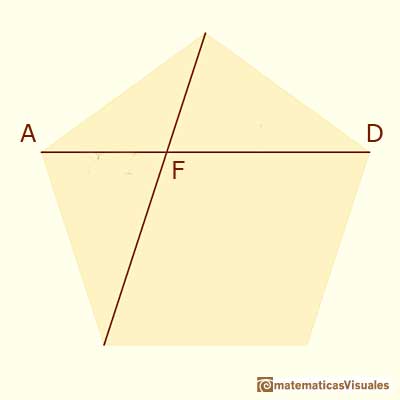
Decimos que las diagonales de un pentágono regular están en proporción áurea con sus lados.
El punto de intersección de dos diagonales de un pentágono regular divide a ambas en la razón áurea (o en 'media y extrema razón').
Suponemos que Pitágoras y los Pitagóricos (alrededor del 500 AC) conocían esta razón porque su símbolo era el pentagrama (un pentágono con sus diagonales), pero la primera referencia escrita que tenemos es en los Elementos de Euclides (alrededor del 300 AC).
Libro VI, Definición 3: "Una línea recta se dice que está cortada en razón extrema y media cuando el total de la linea es al segmento mayor como el mayor es al menor". (Por ejemplo, en Los Elementos de Euclides en la Clark University por D.E. Joyce)
La primera referencia a este tipo de construcción aparece en Libro II, Proposición 11. En este libro Euclides todavía no había definido 'razón' y la proposición se hace en términos de áreas: "Cortar una línea recta dada de modo que el rectángulo contenido por el total y uno de los segmentos es igual al cuadrado del segmento restante". (Los Elementos de Euclides en la Clark University por D.E. Joyce)
Usando nuestra notación:
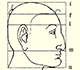
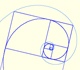
Usando la razón áurea podemos dibujar un pentágono regular, un triángulo áureo y un rectángulo áureo y está relacionada con el icosaedro y el dodecaedro.
Con una tira de papel podemos hacer un nudo y obtener un pentágono y un pentagrama:
Zome es una herramienta excelente para jugar con la razón áurea:
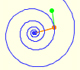
Algunos ejemplos de simetría pentagonal:
REFERENCIAS
SIGUIENTE
MÁS ENLACES
