El dodecaedro regular es un sólido platónico bien conocido desde la Antigüedad.
Leonardo da Vinci dibujó dos dodecaedros para el libro de Luca Pacioli
'La Divina Proporción'.

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su dodecaedro.
Durero publicó el desarrollo plano del dodecaedro por primera vez en 1525.

El primer dibujo del desarrollo plano del dodecaedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.
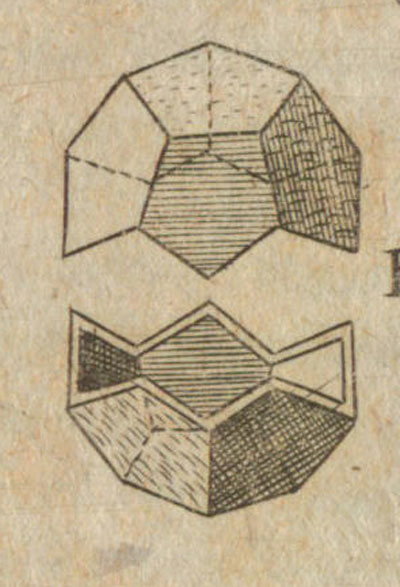
Kepler estuvo interesado en este cuerpo geométrico (por ejemplo, podemos ver este dibujo en su libro
'Harmonices Mundi - La Armonía del mundo', (1619)
(Se puede leer el libro original en Posner Memorial Collection):
Ya hemos estudiado algunas propiedades de este bello poliedro en matemáticasVisuales:

Algunas propiedades de este sólido platónico y su relación con la razón áurea. Construcción de dodecaedros (y otros poliedros relacionados) usando diferentes técnicas.
También sabemos calcular el volumen del dodecaedro (que no parece tan fácil y que luego volveremos a revisar en esta página).

Descomponiendo adecuadamente un dodecaedro podemos obtener fácilmente su volumen.
Ahora vamos a estudiar algunas relaciones entre el dodecaedro y el cubo.
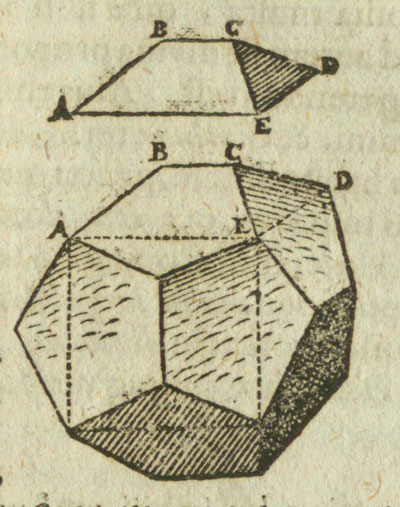
Un cubo se puede inscribir en un dodecaedro de modo que cada arista del cubo esté en una cara del dodecaedro uniendo dos vértices alternos
de cada cara. (Ball and Coxeter, p. 131)
Kepler ya nos mostró esta construcción y vio un dodecaedro como un cubo con seis tejadillos añadidos, uno en cada cara del cubo:
En la aplicación interactiva de esta página podemos ver cómo estos seis tejadillos del dodecaedro se pueden plegar dentro de un cubo:


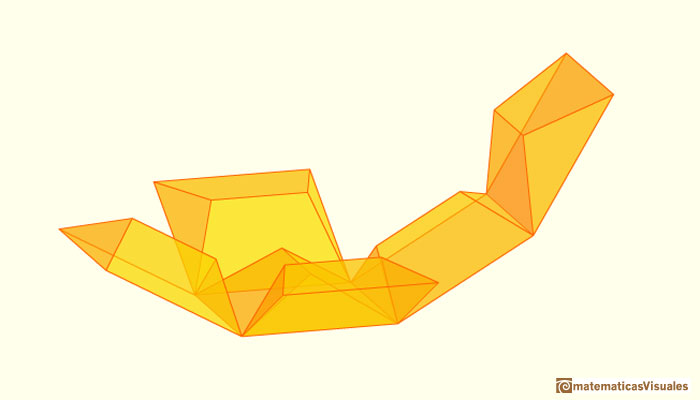


Os animamos a construir vuestra propia figura pues nada sustituye la manipulación de un objeto real:
Vamos a volver a calcular el volumen de un dodecaedro de arista 1. Para ello nos será útil recordar algunas propiedades de la proporción áurea:

La diagonal y el lado de un pentágono regular están en proporción áurea. El punto de intersección de dos diagonales de un pentágono regular divide a ambas en la razón áurea o 'en razón extrema y media'.

Descomponiendo adecuadamente un dodecaedro podemos obtener fácilmente su volumen.
El volumen de un dodecaedro es el volumen de un cubo más seis veces el volumen de un tejadillo.
La longitud de la arista de un cubo es igual a la de la diagonal del pentágono, por lo tanto podemos calcular el volumen del cubo:
Ahora vamos a calcular el volumen del tejadillo.
Una propiedad que nos va a ayudar es que el tejadillo tiene una altura de 1/2.
Podemos construir un tejado con la ayuda de Zome. Esto nos ayuda a ver más claras las medidas.
Podemos considerar que el tejado tiene dos partes:
Por lo tanto, el volumen de un tejadillo es:
Y el volumen del dodecaedro de arista 1 es:
Dentro de un dodecaedro se pueden inscribir cinco cubos. El resultado es esta preciosa figura:
REFERENCIAS
Hugo Steinhaus - 'Mathematical Snapshots' - Oxford University Press - Third Edition.
Magnus Wenninger - 'Polyhedron Models', Cambridge University Press.
Peter R. Cromwell - 'Polyhedra', Cambridge University Press, 1999.
H.Martin Cundy and A.P. Rollet, 'Mathematical Models', Oxford University Press, Second Edition, 1961.
W.W. Rouse Ball and H.S.M. Coxeter - 'Matematical Recreations & Essays', The MacMillan Company, 1947.
 SIGUIENTE
SIGUIENTE

Si plegamos los seis tejadillos del dodecaedro dentro de un cubo queda un espacio vacío en el interior. Este espacio es un dodecaedro no regular con todas sus caras pentagonales iguales. Este dodecaedro es un caso particular de piritoedro.
 ANTERIOR
ANTERIOR

El primer dibujo del desarrollo plano del dodecaedro regular fue publicado por Durero en su libro 'Underweysung der Messung' ('Los cuatro libros de la medida'), el año 1525.
MÁS ENLACES

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación de su dodecaedro.

Algunas propiedades de este sólido platónico y su relación con la razón áurea. Construcción de dodecaedros (y otros poliedros relacionados) usando diferentes técnicas.

Descomponiendo adecuadamente un dodecaedro podemos obtener fácilmente su volumen.

Construcción de cinco tetraedros en un dodecaedro con diferentes técnicas: cartulina, origami, tubos, tensegrity. Justificación de esta preciosa construcción.

Los veinte vértices de un icosaedro están en tres rectángulos áureos. A partir de esta propiedad podemos calcular el volumen del icosaedro.

El ángulo obtuso de las caras rómbicas del dodecaedro rómbico se conoce como ángulo de Maraldi. Solo se necesita un poco de trigonometría básica parar calcularlo.

Estudiando el empaquetamiento de esferas obtenemos el dodecaedro rómbico y el dodecaedro trapezo-rómbico. Su dual es el cuboctaedro girado.

A partir de un conocimiento básico del dodecaedro rómbico se puede calcular rápidamente la densidad del empaquetamiento óptimo de esferas.

Con motivo del Día internacional de las Matemáticas 2020, que se celebra el 14 de Abril, hemos preparado una exposición homenaje a Kepler en relación con el dodecaedro rómbico.

La diagonal y el lado de un pentágono regular están en proporción áurea. El punto de intersección de dos diagonales de un pentágono regular divide a ambas en la razón áurea o 'en razón extrema y media'.

Podemos dibujar un pentágono regular dado uno de sus lados construyendo la razón áurea con regla y compás.
En su libro 'Underweysung der Messung' Durero dibujó un pentágono no regular con regla y compás con apertura fija. Es una construcción simple y una muy buena aproximación de un pentágono regular.

A partir de la definición de Euclides de la división de un segmento en su razón media y extrema introducimos una propiedad de los rectángulos áureos y deducimos la ecuación y el valor de la proporción áurea.

Un rectángulo áureo se puede descomponer en un cuadrado y otro rectángulo áureo.

La espiral áurea se contruye a partir de rectángulos áureos y es una aproximación simple a una espiral equiangular.





























 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR




























