
El siguiente vídeo nos muestra las ideas principales de esta página:
Nos podemos imaginar que el interés por los panales de las abejas ha acompañado a la Humanidad desde tiempo inmemorial. Solemos citar a Pappus de Alejandría (hacia el año 320) como el primer matemático interesado en la forma de los panales de abeja del que nos ha llegado noticia. Él pensó que el prisma hexagonal era una solución óptima para las abejas. Es decir, que esta estructura hexagonal que tienen los panales minimiza la cantidad de cera que las abejas necesitan para construir sus celdillas. Estas celdas contienen más miel en relación con su superficie.

Pappus escribió:
"Las abejas conocen el hecho, que está a su servicio, de que el hexágono es mayor que el cuadrado y que el triángulo y que contendrá más miel para la misma cantidad de material usado para construir estas figuras". (Podemos leer más sobre Pappus en la nota 16 del libro 'The Six Cornered Snowflake' o en el libro de Sir Thomas Heath 'A History of Greek Mathematics' [Dover, 1981]).
Pappus consideró solo la forma del prisma hexagonal pero no la forma del fondo de la celda. Este fondo de la celdilla está formado por tres rombos iguales.
El problema de que el prisma hexagonal es óptimo o isoperimétrico se conoce con la Conjetura del Panal. Esta conjetura permaneció sin probar hasta mediados del siglo XX (Laszlo Fejes Toth, Thomas Hale). Resultó ser un problema fácil de enunciar pero muy difícil de probar. Además, Toth probó que las bases de las celdillas cerradas con tres rombos no eran formas óptimas, después de todo. Pero esto es adelantar acontecimientos.
Después de que Kepler descubriera el dodecaedro rómbico observando la base de las celdas de las abejas, otros matemáticos y científicos estuvieron interesados en el estudio de cómo las abejas construyen el fondo de sus celdas.
Giacomo Maraldi (hacia 1712) retoma el interés por la forma de la base de las celdas de las abejas. Quizás las aportaciones de Kepler han caído en el olvido. Obtiene las medidas de los ángulos de las caras rómbicas con precisión. En teoría lo hace midiendo realmente panales de abejas. En sus investigaciones usó colmenas de vidrio transparente para poder observar el interior (parece que fue el inventor de esta técnica). Actualmente se piensa que, con los medios de la época, no pudo hacerlo de este modo. El ángulo obtuso de este rombo recibe el nombre de ángulo de Maraldi en su honor.
Durante el siglo XVIII hay interés por comprobar si las abejas optimizan el consumo de cera al elegir tres rombos como base de sus celdas. Es decir, para un determinado volumen de la celda hexagonal ¿cuál es la manera de cerrarla de modo que la superficie (el consumo de cera) sea mínimo? Estos problemas de optimización pueden ser muy complicados. Vamos a ver una primera aproximación.
El entomólogo francés Réaumur está interesado en esta cuestión y le plantea el problema a Samuel Koening, un joven matemático suizo. Dada una celda hexagonal cerrada por tres rombos iguales, ¿cuál es la configuración que requiere la menor cantidad de material para su construcción?
En 1739, Koening escribió una carta a Réaumur con su respuesta que era similar (pero no exactamente igual) a la que había dado Maraldi. Parece que esta carta no fue publicada y se ha perdido. No sabemos cómo Koening estudió el problema. Pero el caso es que había una pequeña discrepancia sobre la medida de esos ángulos.
Unos años después, en 1743, el matemático escocés Colin Maclaurin (1698-1746) escribió 'On the Bases of the Cells wherein the Bees deposite their Honey' (que podemos traducir en 'Sobre las bases de las celdas donde las abejas depositan su miel'). Maclaurin zanja la cuestión y lo hace usando métodos puramente geométricos (y no las técnicas del cálculo diferencial que él ya conocía). Esto no era raro en la época.
Las medidas correctas eran las de Maraldi. ¿Cuál fue el error de Koening? Parece que el error procede de un error en las tablas que Koening estaba usando. Se cuenta como anécdota que este error pudo corregirse gracias al estudio de este asunto, aparentemente poco importante, como es el de la forma de las celdas de las abejas. Sin embargo, esas tablas eran las mismas que usaban los marinos para calcular su posición y la corrección del error bien pudo salvar muchas vidas en el mar.
En esta página vamos a estudiar este problema de optimización simplificado: queremos cerrar el prisma hexagonal como parece que hacen las abejas, usando tres rombos iguales.
Entonces, ¿cuál es la forma de estos tres rombos iguales que cierran el prisma hexagonal con la mínima superficie?
Podemos jugar con el applet y ver diferentes maneras de cerrar el prisma hexagonal, más apuntado o más aplanado:
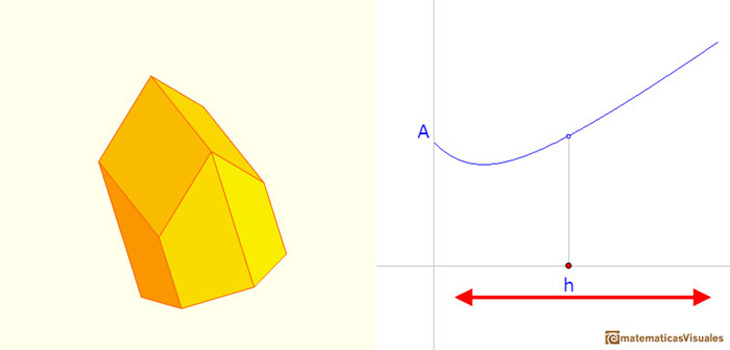
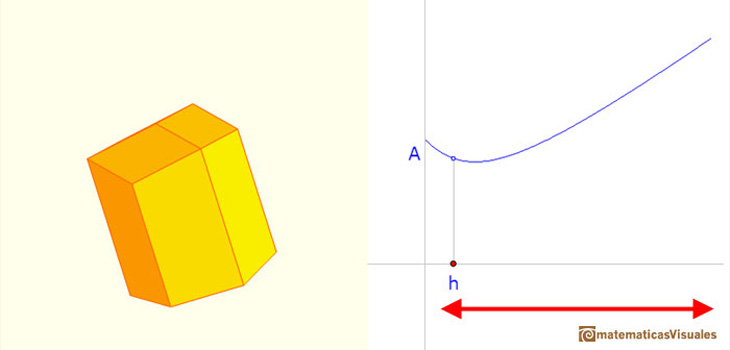
Si cambiamos la forma, la superficie cambia también.


Y queremos minimizar esa superficie.
Sin embargo, cuando cambiamos la forma de la figura, el volumen no cambia.
En el applet, podemos abrir y cerrar el vértice para ver la razón:
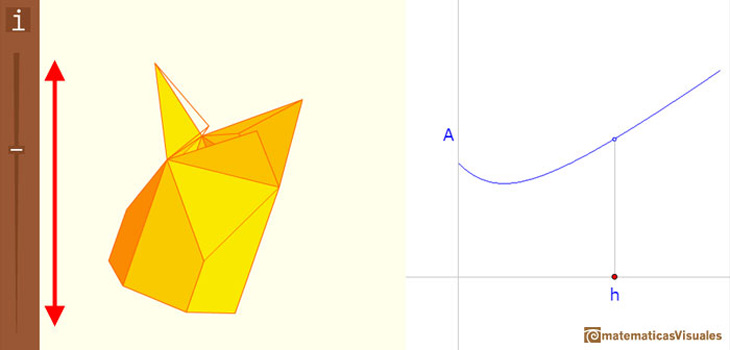
Para cerrar la celda cortamos tres pirámides del prisma hexagonal y las ponemos juntas para formar el vértice (que Kepler llamó la quilla). Entonces el volumen es el mismo pues lo que quitas de un lado lo pones en otro.


En resumen, cuando cambiamos la forma del cerramiento el volumen de la figura no cambia pero si cambia la superficie. Y la superficie es lo que queremos minimizar.
Podríamos calcular la superficie lateral del prisma hexagonal pero no vamos a necesitar ese cálculo. Nuestro problema no dependerá de la altura del prisma y podemos suponer simplemente que es suficientemente alto. Nuestro problema está relacionado con los tres rombos que cierran el prisma.
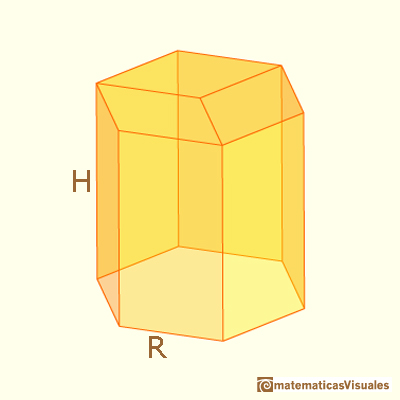
R es el radio de la circunferencia circunscrita al hexágono y también es la longitud de su lado y h es la altura desde el vértice del rombo a un vértice del hexágono. h es nuestra variable independiente. Cambiando h cambiamos la forma y la superficie necesaria para cerrar el prisma (pero no el volumen de la figura).
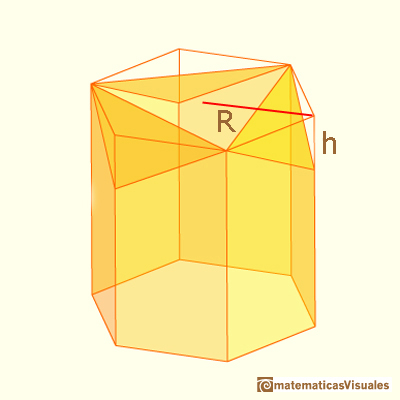
Podemos hacer nuestro cálculos considerando sólo uno de los rombos puesto que los tres son iguales.
Si empezamos con dos de los rectángulos laterales del prisma lo primero que podemos hacer es cortar dos triángulos rectánguos. Estos triángulos t tienen base R y altura h.
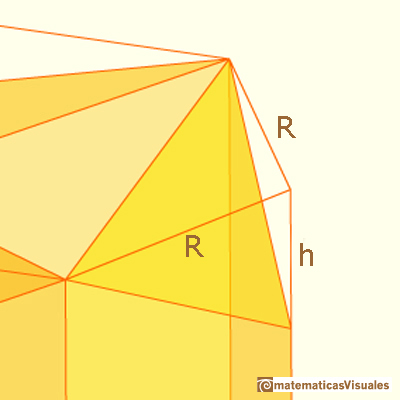
Entonces el área de estos triángulos t es:
Cada uno de los rombos esta formado por dos triángulos r. Tienen base d y altura a.
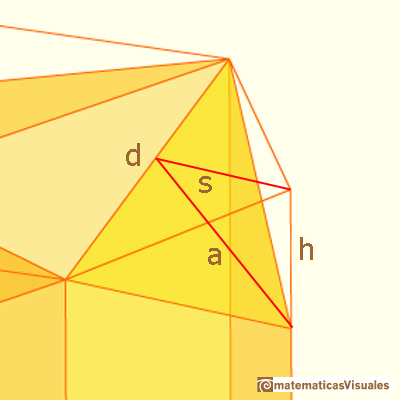
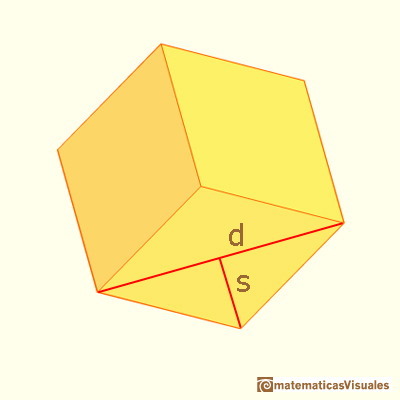
La diagonal d es fácil de calcular pues es una diagonal del hexágono:
Necesitamos s que está relacionado con R, el radio de la circunferencia circunscrita:
Ahora podemos aplicar el teorema de Pitágoras para calcular a:
Entonces el área del triángulo r es:
Podemos simplificar un poco:
El área del rombo que queremos añadir es el doble del área de este triángulo.
Ahora ya podemos calcular el área de nuestra figura. Consideremos solo uno de los rombos y lo que haces es quitar dos triángulos t y añadir dos triángulos r.
La función que queremos optimizar (sin considerar el área lateral del prisma que no es relevante y pensando en solo un rombo) es:
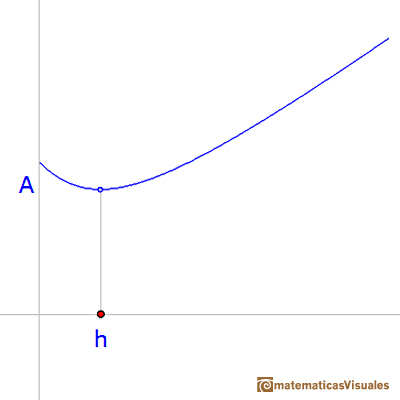
Para obtener el mínimo de esta función podemos usar la derivada:
Y el mínimo es:
Podemos comprobar la relación que hay entre las dos diagonales de estos rombos:
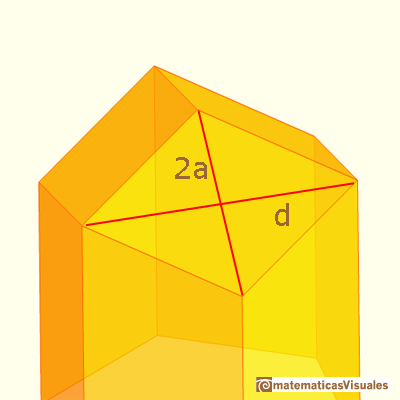
Este rombo es un rombo especial. Con doce de estos rombos se puede construir un poliedro que llamamos dodecaedro rómbico.
Johannes Kepler fue el primer matemático que escribió sobre el dodecaedro rómbico y pensó que las abejas cierran sus celdillas con rombos que son como los del dodecaedro rómbico.
"Intrigado por estos rombos [los tres rombos iguales que forman la quilla de una celda en un panal] empecé a miran en la geometría para ver si algún cuerpo que se pareciera a los cinco sólidos regulares y a los catorce sólidos Arquimedianos podrían construirse exclusivamente con rombos. Descubrí dos, uno relacionado con el cubo y el octaedro, el otro con el dodecaedro y el icosaedro. (El mismo cubo puede ser considerado un tercero, puesto que es como dos tetraedros unidos)." (Johannes Kepler, 'De Nive Sexangula'). [Nota: Actualmente se considera que hay trece sólidos arquimedianos y no catorce como dice Kepler].

En el siguiente vídeo podemos ver la celda de las abejas con transparencia:
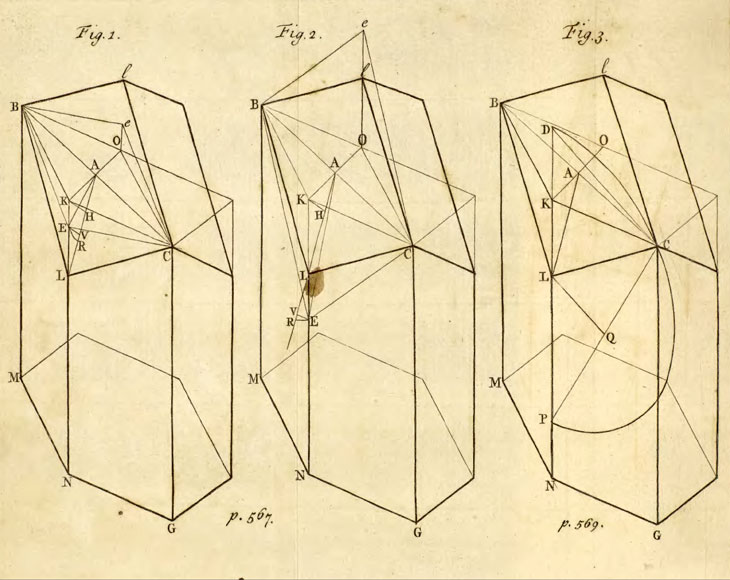
El siguiente dibujo es de la carta de Colin Maclaurin 'On the Bases of the Cells wherein the Bees deposite their Honey'.

Pero, ¿realmente este modo teórico de cerrar las celdas de las abejas es óptimo?. László Fejes Tóth el artículo 'What the bees know and what they do not know' ('Lo que las abejas saben y lo que no') in 1964. En este artículo propone un cierre de la celda de las abejas que es un poco mejor (y que recuerda a las caras del octaedro truncado). Escribió:
En vez de cerrar el fondo de la celda con tres rombos, como hacen las abejas, es siempre más eficiente usar dos hexágonos y dos rombos.
Esta es una ilustración tomada de ese artículo:
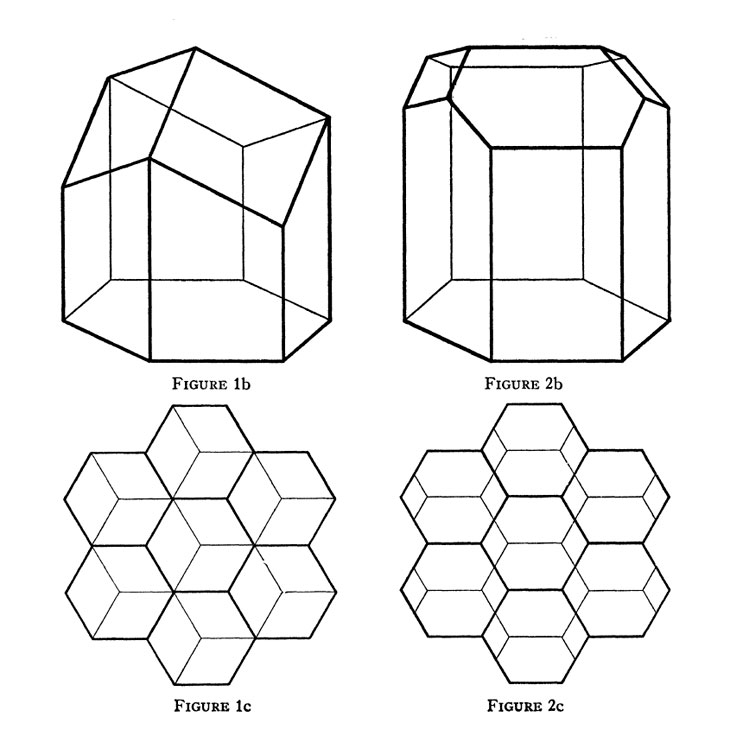
Fejes Tóth concluyó:
Tenemos que admitir que todo esto no tiene consecuencias prácticas. Si las abejas construyeran estas celdas ahorrarían por cada celda menos de 0,35% del área de una apertura (y mucho menor porcentaje de la superficie de una celda). Por otra parte, las paredes de las celdas tienen un grosor que no debemos despreciar. Además, las aperturas de las celdas están lejos de ser exactamente regulares. Además, el estilo de construir de las abejas es claramente más sencillo que el que se escribe arriba. Por lo tanto, esto no es suficiente para socavar la convicción de que las abejas tienen una intuición geométrica profunda.
Llegados a este punto, nos podríamos plantear ¿cómo construyen realmente las abejas sus celdas?
No es tarea tan sencilla como pudiera parecer. Para empezar, los apicultores modernos ayudan a las abejas a construir sus celdas. En cada marco de la colmena les colocan una base de cera con los rombos estampados para que ellas se ahorren esa tarea. A partir de esa plancha de cera, las abejas 'estiran' las celdas hexagonales. Hay que tener en cuenta que la producción de cera es un trabajo muy costoso para las abejas.
Necesitamos encontrar una colmena salvaje donde las abejas hayan construido sus celdas de una manera natural, sin intervención humana.
Lo conseguí gracias a mi amigo Luis Larriba. Él es ceramista, experto en cerámica histórica y buen aficionado a la apicultura. Juntos fuimos a un lugar cerca de Tartanedo (un pueblo en Guadalajara, España) para ver cómo trabajan las abejas en un entorno natural. En una pequeña construcción, llamada 'colmenar de hornos', las abejas construyen su panal:
Allí pude coger un panal natural y limpio. Cuidadosamente destruí los prismas hexagonales para ver la base de varias celdas.
Las siguientes fotografías reflejan la conclusión: podemos ver que algunas bases de las celdas están formadas por tres rombos bastante perfectos. Pero otras son diferenes y podemos ver que están formadas por dos hexágonos y dos rombos.

REFERENCIAS
 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR
MÁS ENLACES



































