
El concepto de semejanza de figuras es muy importante en Geometría y sus aplicaciones prácticas están presentes en nuestra vida cotidiana y son fundamentales para la ciencia y la técnica. Por ejemplo: planos o mapas, modelos a escala o maquetas.
Intuitivamente, dos figuras son semejantes si 'tienen la misma forma', lo que suele cambiar es el tamaño.
Cada punto, segmento o elemento de una figura tiene su correspondiente elemento en una figura semejante.
Nos parece bastante natural preguntarnos cómo cambian las longitudes de elementos correspondientes de figuras semejantes, por ejemplo, los lados. Pero también, si procede, cómo cambian las áreas y los volúmenes de figuras semejantes.
El caso de los triángulos es particularmente sencillo: Dos triángulos son semejantes, tienen la misma forma, si sus ángulos son respectivamente iguales. Entonces se cumple que sus lados respectivos son proporcionales. (Euclides, VI.4). También podremos escribir proporciones considerando cualquier segmento de un triángulo y su correspondiente en el otro.
En particular, como nos podemos imaginar, todos los triángulos equiláteros son semejantes.
Vamos a considerar el lado y la altura de cada uno de los triángulos equiláteros. Los lados son a y b y las alturas correspondientes las denotamos h(a) y h(b)
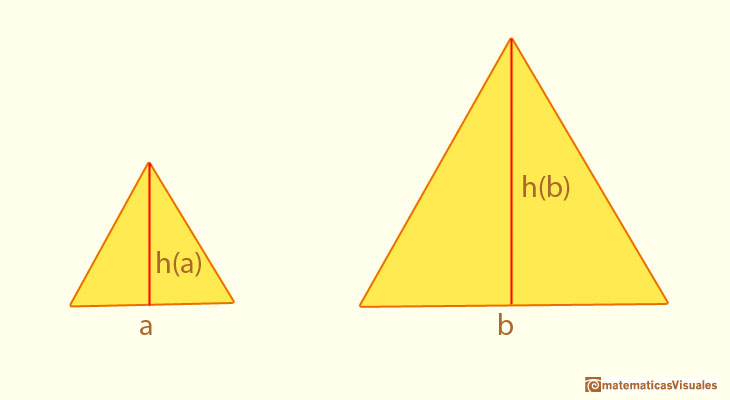
Podremos escribir una proporción:
Lo que estamos expresando con esta proporción es algo muy simple y muy potente. Un triángulo es una ampliación (o reducción) del otro. Si el segundo triángulo tiene el lado el doble de largo que el primero entonces su altura también será el doble. Si un triángulo tiene el lado que es la mitad que el otro entonces su altura también será la mitad. Es muy sencillo e intuitivo.
Si a es 1 y b es 2 podemos escribir:
Despejando:
Si a es 1 y b es 7 escribiríamos:
En general:
También podríamos escribir:
Lo que nos están diciendo estas expresiones es que BASTA CON CALCULAR UNA SOLA VEZ LA ALTURA DE UN TRIÁNGULO EQUILÁTERO para que sepamos cuál es la altura de cualquier triángulo equilátero a partir de su lado. No tenemos que hacerlo para cada caso, solo una vez. Aplicando esta propiedad de la semejanza nos vamos a ahorrar trabajo.
Vamos pues a calcular la altura de un triángulo equilátero.
Podemos elegir el que queramos, por lo tanto, vamos a calcular la altura del triángulo equilátero que nos parezca más sencillo.
Para calcular esa altura usaremos el Teorema de Pitágoras.
Como podemos elegir, ¿cuál es un buen triángulo para hacer esto cálculos?¿Cuál es preferible, el de lado 1 o el de lado 2?
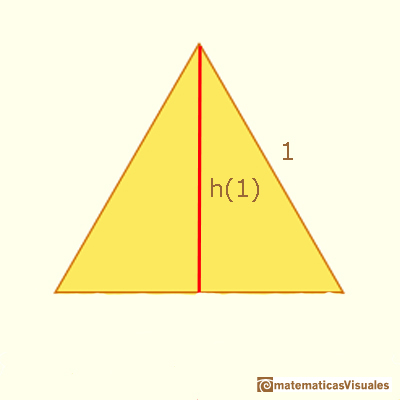
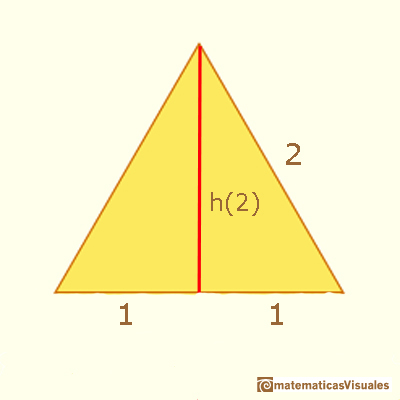
El triángulo equilátero más sencillo para estos cálculos es el de lado 2 pues, al aplicar el Teorema de Pitágoras, no vamos a usar fracciones.
Entonces, la altura de un triángulo de lado 1 es:
Sin hacer ningún cálculo más ya sabemos responder a estas cuestiones:
En general, se verifica esta relación entre la altura de un triángulo equilátero de lado b y el de lado 1:
¿Qué ocurre con las áreas?
Nos encontramos con una situación parecida: BASTA SABER CALCULAR EL ÁREA DE UN TRIÁNGULO EQUILÁTERO SENCILLO, HACERLO UNA SOLA VEZ, para poder deducir el área de cualquier triángulo equilátero.
Pero la relación que hay es un poco diferente. Vamos a ver por qué.
El área de un triángulo equilátero de lado 2 es muy sencilla:
Si nos fijamos en la siguiente ilustración, un triángulo equilátero que tenga un lado que sea el doble que otro cumple que su área es cuatro veces más grande.

Por lo tanto, el área de un triángulo de lado 1 es:
Si su lado fuera el triple, el área sería 9 veces más grande, y así sucesivamente.
En general se cumple que las áreas de triángulos semejantes son entre sí como el cuadrado de la razón de sus lados correspondientes (Euclides, VI.19).
Para el caso de los triángulos equiláteros de lados a y b podríamos escribir:
Haciendo b = 1 resulta:
Por ejemplo, sabemos calcular el área de un triángulo equilátero de lado 7:
PARA SABER MÁS
En muchos libros de Geometría podremos estudiar propiedades que se deducen de la semejanza de triángulos.
Por ejemplo, en el libro de Coxeter, 'Fundamentos de Geometría', en las páginas 30 y 31 podemos ver algunas de estas propiedades y, en particular, una demostración del Teorema de Pitágoras muy sencilla que se deduce directamente de la relación entre áreas de triángulos semejantes.
Estas propiedades que relacionan longitudes y áreas de triángulos semejantes se aplican también a figuras semejantes en general.
Para que dos polígonos, por ejemplo, tengan 'la misma forma' se tiene que exigir que sus ángulos correspondientes sean iguales y sus lados correspondientes proporcionales.
Se verifican las mismas relaciones. Si denotamos por L una determinada longitud de una figura, (un ejemplo podría ser la diagonal de un cuadrado de lado a en relación con la diagonal de un cuadrado de lado 1), entonces podríamos escribir:
Si denotamos por A el área de una determinada figura entonces la relación se podría escribir:
INVESTIGA
Johnatan Swift escribió 'Los viajes de Gulliver'. En uno de sus viajes llega al país de Liliput que son enanos desde el punto de vista de Gulliver. Gulliver es 12 veces más alto. Los matemáticos liliputienses tienen claro cuántas capas liliputienses hacen falta para hacerle una capa a Gulliver.
¿Sabrías hacer este cálculo y escribirlos con la notación que estamos usando?
INVESTIGA
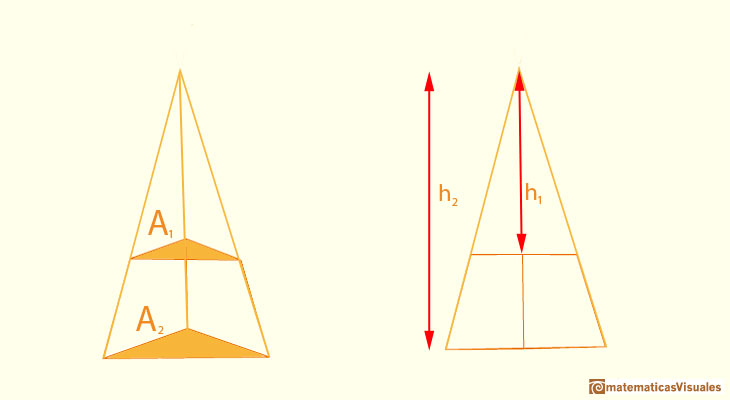
La siguiente ilustración representa una proyección. Llamamos a esta transformación una homotecia. Nos la podemos imaginar en el plano o en el espacio. Los dos triángulos son semejantes. Los podemos ver como las dos bases de una pirámide truncada.
¿Sabrías relacionar las áreas de las dos bases con sus alturas respectivas?
El razonamiento también se puede hacer con otros polígonos o círculos.
INVESTIGA
¿Qué relación piensas que habrá entre los volúmenes de dos figuras semejantes?
REFERENCIAS
 SIGUIENTE
SIGUIENTE
MÁS ENLACES














































