|
|
|
The Volume of the Truncated Octahedron
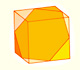
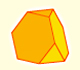
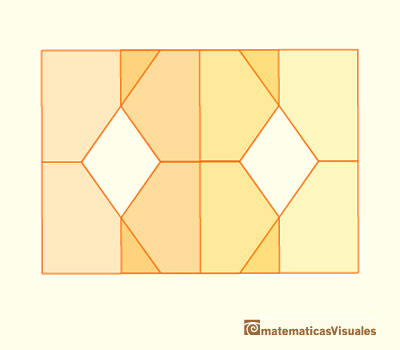
The truncated octahedron is a space-filling polyhedron. The truncated octahedron is an Archimedean polyhedron and you can think it as a octahedron from which you have removed six half octahedra.
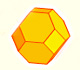
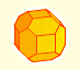
The truncated octahedron is an Archimedean solid. It has 8 regular hexagonal faces and 6 square faces. Its volume can be calculated knowing the volume of an octahedron.
Here we can see another point of view: A truncated octahedron is built by eight half cubes. This relation between the cube and the truncated octahedron can help us to understand the space-filling property of this beautiful polyhedron.
We have already calculated the volume of half a cube. Then, the volume of a truncated octahedron is eight times the volume of half a cube:
You can play with the transparency in this mathlet version
REFERENCES
Hugo Steinhaus, Mathematical Snapshots, Dover Publications (third edition, 1999)
We can read some pages of this book in Google Books:
Mathematical Snapshots by Hugo Steinhaus.
Magnus Wenninger - 'Polyhedron Models', Cambridge University Press.
Peter R. Cromwell - 'Polyhedra', Cambridge University Press, 1999.
H.Martin Cundy and A.P. Rollet, 'Mathematical Models', Oxford University Press, Second Edition, 1961.
NEXT
These polyhedra pack together to fill space, forming a 3 dimensional space tessellation or tilling.
PREVIOUS
We can cut in half a cube by a plane and get a section that is a regular hexagon. Using eight of this pieces we can made a truncated octahedron.
MORE LINKS
The truncated octahedron is an Archimedean solid. It has 8 regular hexagonal faces and 6 square faces. Its volume can be calculated knowing the volume of an octahedron.
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the truncated octahedron.
The volume of an octahedron is four times the volume of a tetrahedron. It is easy to calculate and then we can get the volume of a tetrahedron.
The volume of a tetrahedron is one third of the prism that contains it.
The first drawing of a plane net of a regular tetrahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .
Some properties of this platonic solid and how it is related to the golden ratio. Constructing dodecahedra using different techniques.
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the cuboctahedron.
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the dodecahedron.
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the stellated octahedron (stella octangula).
The volume of an octahedron is four times the volume of a tetrahedron. It is easy to calculate and then we can get the volume of a tetrahedron.
Some properties of this platonic solid and how it is related to the golden ratio. Constructing dodecahedra using different techniques.
The stellated octahedron was drawn by Leonardo for Luca Pacioli's book 'De Divina Proportione'. A hundred years later, Kepler named it stella octangula.
The compound polyhedron of a cube and an octahedron is an stellated cuboctahedron.It is the same to say that the cuboctahedron is the solid common to the cube and the octahedron in this polyhedron.
The truncated tetrahedron is an Archimedean solid made by 4 triangles and 4 hexagons.
When you truncate a cube you get a truncated cube and a cuboctahedron. If you truncate an octahedron you get a truncated octahedron and a cuboctahedron.
You can chamfer a cube and then you get a polyhedron similar (but not equal) to a truncated octahedron. You can get also a rhombic dodecahedron.