|
|
|
Stellated Cuboctahedron
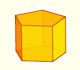
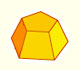
The cuboctahedron is an Archimedean solid. It was drawn by Leonardo da Vinci for Luca Pacioli's book 'De divina proportione'.
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the cuboctahedron.
We can see this polyhedron as a truncated cube or as a truncated octahedron and we can easily calculate its volume.
A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of a cube.
A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of an octahedron.
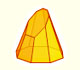
The first stellation of the cuboctahedron is the compound of a cube and its dual octahedron, with the vertices of the cuboctahedron located at the midpoints of the edges. It is the same to say that the solid common to both the cube and the octahedron in a cube-octahedron compound is a cuboctahedron.
You can build the stellated cuboctahedron using Zome:
Can you calculate the relative sizes of these polyhedra?
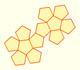
The vertices of a stellated cuboctahedron are the vertices of a rhombic dodecahedron (that is the dual polyhedra of a cuboctahedron).
REFERENCES
Hugo Steinhaus - Mathematical Snapshots - Oxford University Press - Third Edition (p. 197)
Magnus Wenninger - 'Polyhedron Models', Cambridge University Press.
Peter R. Cromwell - 'Polyhedra', Cambridge University Press, 1999.
H.Martin Cundy and A.P. Rollet, 'Mathematical Models', Oxford University Press, Second Edition, 1961 (p. 87).
W.W. Rouse Ball and H.S.M. Coxeter - 'Matematical Recreations & Essays', The MacMillan Company, 1947.
Luca Pacioli - De divina proportione - (La divina proporción) Ediciones Akal, 4ª edición, 2004. Spanish translation by Juan Calatrava.
NEXT
The stellated octahedron was drawn by Leonardo for Luca Pacioli's book 'De Divina Proportione'. A hundred years later, Kepler named it stella octangula.
PREVIOUS
A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of an octahedron.
MORE LINKS
A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of a cube.
The volume of an octahedron is four times the volume of a tetrahedron. It is easy to calculate and then we can get the volume of a tetrahedron.
The volume of a tetrahedron is one third of the prism that contains it.
The first drawing of a plane net of a regular tetrahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .
We study different prisms and we can see how they develop into a plane net. Then we explain how to calculate the lateral surface area.
Plane nets of prisms with a regular base with different side number cut by an oblique plane.
We study different cylinders and we can see how they develop into a plane. Then we explain how to calculate the lateral surface area.
We study different cylinders cut by an oblique plane. The section that we get is an ellipse.
Plane net of pyramids and pyramidal frustrum. How to calculate the lateral surface area.
Plane net of pyramids cut by an oblique plane.
Plane developments of cones and conical frustum. How to calculate the lateral surface area.
Plane developments of cones cut by an oblique plane. The section is an ellipse.
The first drawing of a plane net of a regular dodecahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .
The twelve vertices of an icosahedron lie in three golden rectangles. Then we can calculate the volume of an icosahedron
Some properties of this platonic solid and how it is related to the golden ratio. Constructing dodecahedra using different techniques.
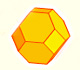
The truncated octahedron is an Archimedean solid. It has 8 regular hexagonal faces and 6 square faces. Its volume can be calculated knowing the volume of an octahedron.
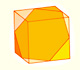
We can cut in half a cube by a plane and get a section that is a regular hexagon. Using eight of this pieces we can made a truncated octahedron.
Using eight half cubes we can make a truncated octahedron. The cube tesselate the space an so do the truncated octahedron. We can calculate the volume of a truncated octahedron.
These polyhedra pack together to fill space, forming a 3 dimensional space tessellation or tilling.
The truncated octahedron is an Archimedean solid. It has 8 regular hexagonal faces and 6 square faces. Its volume can be calculated knowing the volume of an octahedron.
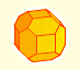
You can chamfer a cube and then you get a polyhedron similar (but not equal) to a truncated octahedron. You can get also a rhombic dodecahedron.
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the truncated octahedron.
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the cuboctahedron.
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the dodecahedron.
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the stellated octahedron (stella octangula).
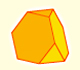
The truncated tetrahedron is an Archimedean solid made by 4 triangles and 4 hexagons.
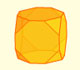
When you truncate a cube you get a truncated cube and a cuboctahedron. If you truncate an octahedron you get a truncated octahedron and a cuboctahedron.