A regular tetrahedron is a polyhedron with four equilateral triangular faces,
four vertices and six edges.
It is a Platonic solid.

The volume of a tetrahedron is one third of the prism that contains it.
It was Durer the first to publish plane nets of polyhedra. In his
book 'Underweysung der Messung' ('Four Books of Measurement', published in 1525) the author draw plane developments of several
Platonic and Archimedean solids, for example, this regular tetrahedron:
"[Durer] He introduces a technique of conveying information about three-dimensional objects on a flat surface via
paper-folding which in modern times is called a net. The method involves developing the surface of a polyhedron onto a plane
sheet of paper so that the resulting figure can be cut out as a single connected piece then folded up to form a three-dimensional
model of the original polyhedron". (Cromwell, p.127)
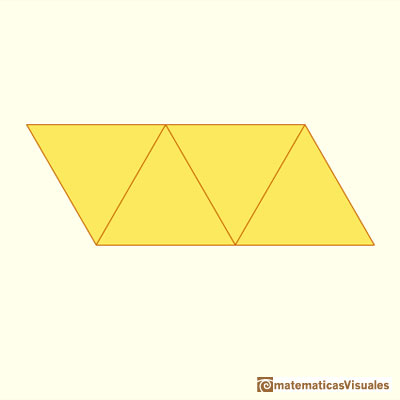
Playing with the application you can see how a tetrahedron develops into a plane net. This is a very typical plane net of a tetrahedron but it is
different from the plane net that Durer drew:
In the next application we can see the plane development of a tetrahedron as Durer did:
REFERENCES
Erwin Panofsky - The Life and Art of Albrecht Dürer - Princeton University Press
Dan Pedoe - Geometry and the Liberal Arts - St. Martin's Press (p. 76)
Hugo Steinhaus - Mathematical Snapshots - Oxford University Press - Third Edition (p. 197)
Magnus Wenninger - 'Polyhedron Models', Cambridge University Press.
Peter R. Cromwell - 'Polyhedra', Cambridge University Press, 1999.
H.Martin Cundy and A.P. Rollet, 'Mathematical Models', Oxford University Press, Second Edition, 1961 (p. 87).
W.W. Rouse Ball and H.S.M. Coxeter - 'Matematical Recreations & Essays', The MacMillan Company, 1947.
MORE LINKS

The first drawing of a plane net of a regular octahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .

The volume of an octahedron is four times the volume of a tetrahedron. It is easy to calculate and then we can get the volume of a tetrahedron.
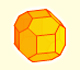
You can chamfer a cube and then you get a polyhedron similar (but not equal) to a truncated octahedron. You can get also a rhombic dodecahedron.
We study different prisms and we can see how they develop into a plane net. Then we explain how to calculate the lateral surface area.

Plane nets of prisms with a regular base with different side number cut by an oblique plane.

We study different cylinders and we can see how they develop into a plane. Then we explain how to calculate the lateral surface area.

We study different cylinders cut by an oblique plane. The section that we get is an ellipse.
Plane net of pyramids and pyramidal frustrum. How to calculate the lateral surface area.
Plane net of pyramids cut by an oblique plane.

Plane developments of cones and conical frustum. How to calculate the lateral surface area.

Plane developments of cones cut by an oblique plane. The section is an ellipse.
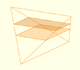
In his article 'Two Surprising Theorems on Cavalieri Congruence' Howard Eves describes an interesting tetrahedron. In this page we calculate its cross-section areas and its volume.

Special sections of a tetrahedron are rectangles (and even squares). We can calculate the area of these cross-sections.
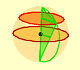
We want to calculate the surface area of sections of a sphere using the Pythagorean Theorem. We also study the relation with the Geometric Mean and the Right Triangle Altitude Theorem.



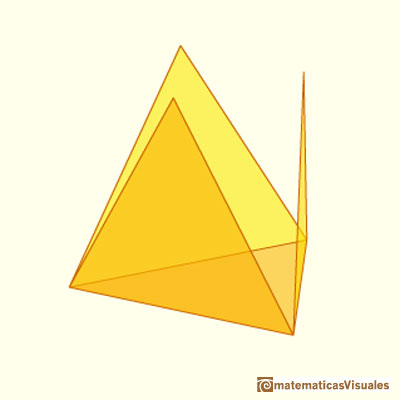


 NEXT
NEXT





















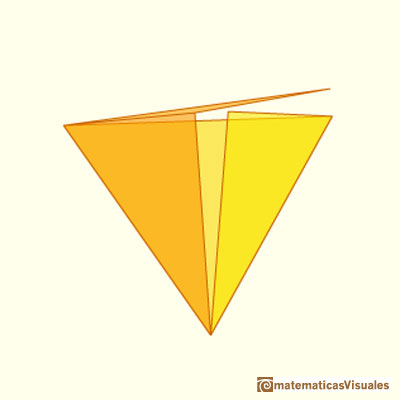




 PREVIOUS
PREVIOUS






