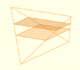
We have already seen that the volume of a tetrahedron (in general, not regular) we can obtain joining the diagonals of the faces of a parallelepiped is a third the volume of that parallelepiped.

In this applet we can see the sections of a tetrahedron built from a parallelepiped with square base.

In the initial position, the applet displays a regular tetrahedron cut in half by a square section. It is a well-known puzzle formed by these two pieces alike.

It is easy to build these two pieces and make the puzzle (each piece is a compound of two small tetrahedra and half octahedron):

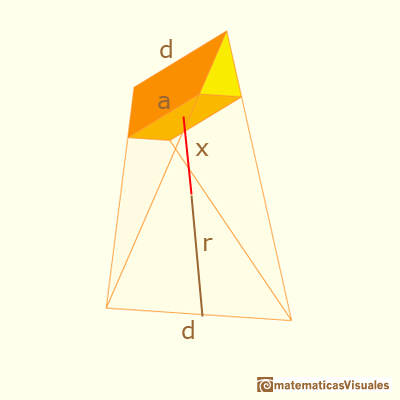
We are considering these cross-sections of a tetrahedron that are rectangles in general. In the middle, the cross-section is a square.

You can calculate the area of those sections.

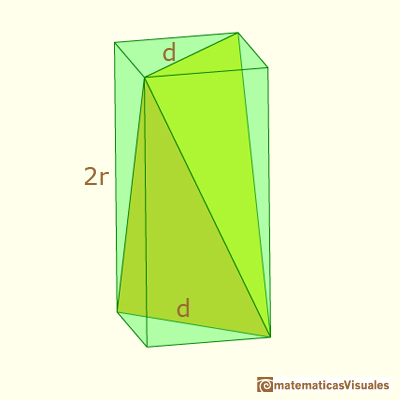
Each of these tetrahedra are inside of a prism with square base:

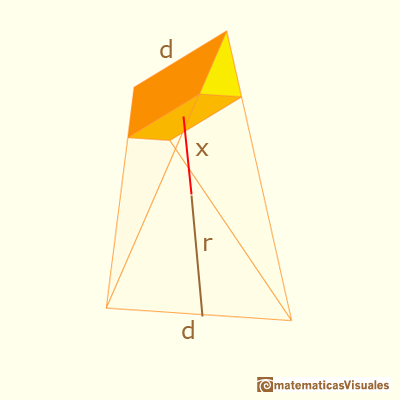
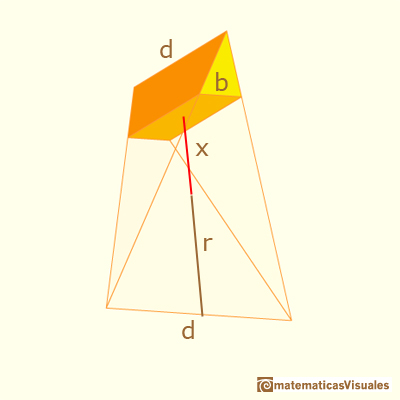
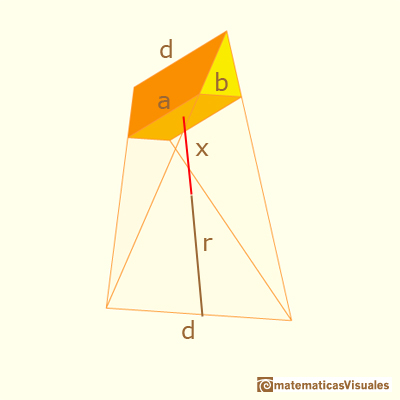
If x is the distance between the center and the section:

You can calculate the side a:

And the side b of the section:

Now the area of the section is:

You can do the same calculation in an interesting particular case on the page devoted to the sections of Howard Eves's tetrahedron.

MORE LINKS

Plane developments of geometric bodies: Tetrahedron

The first drawing of a plane net of a regular tetrahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .

Sections in the sphere

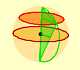
We want to calculate the surface area of sections of a sphere using the Pythagorean Theorem. We also study the relation with the Geometric Mean and the Right Triangle Altitude Theorem.

Surprising Cavalieri congruence between a sphere and a tetrahedron

Howard Eves's tetrahedron is Cavalieri congruent with a given sphere. You can see that corresponding sections have the same area. Then the volumen of the sphere is the same as the volume of the tetrahedron. And we know how to calculate this volumen.

Cavalieri: The volume of a sphere

Using Cavalieri's Principle we can calculate the volume of a sphere.

Campanus' sphere and other polyhedra inscribed in a sphere

We study a kind of polyhedra inscribed in a sphere, in particular the Campanus' sphere that was very popular during the Renaissance.

Leonardo da Vinci:Drawing of a SEPTUAGINTA made to Luca Pacioli's De divina proportione.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the Campanus' sphere.

Kepler: The Area of a Circle

Kepler used an intuitive infinitesimal approach to calculate the area of a circle.

Archimedes and the area of an ellipse: an intuitive approach

In his book 'On Conoids and Spheroids', Archimedes calculated the area of an ellipse. We can see an intuitive approach to Archimedes' ideas.

Archimedes and the area of an ellipse: Demonstration

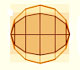
In his book 'On Conoids and Spheroids', Archimedes calculated the area of an ellipse. It si a good example of a rigorous proof using a double reductio ad absurdum.

Archimedes' Method to calculate the area of a parabolic segment

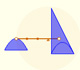
Archimedes show us in 'The Method' how to use the lever law to discover the area of a parabolic segment.

Plane developments of geometric bodies (1): Nets of prisms

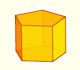
We study different prisms and we can see how they develop into a plane net. Then we explain how to calculate the lateral surface area.

Plane developments of geometric bodies (3): Cylinders

We study different cylinders and we can see how they develop into a plane. Then we explain how to calculate the lateral surface area.

Plane developments of geometric bodies (5): Pyramid and pyramidal frustrum

Plane net of pyramids and pyramidal frustrum. How to calculate the lateral surface area.

Plane developments of geometric bodies (7): Cone and conical frustrum

Plane developments of cones and conical frustum. How to calculate the lateral surface area.

Plane developments of geometric bodies: Dodecahedron

The first drawing of a plane net of a regular dodecahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .