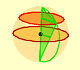
This kind of polyhedra that are inscribed in a sphere was well know by Euclid. In proposition 17 of book XII Euclid shows how to construct a polyhedron sandwiched between two concentric spheres.
During the Middle Ages, Campanus of Novara (1220-1296) wrote a very popular version of Euclid's Elements. Campanus used this construction to describe a 72-faced polyhedron. This polyhedron was very popular during the Renaissance and was known as Campanus´ sphere.
Leonardo da Vinci draw this polyhedron to Luca Pacioli's book 'De Divina Proportione'.

If you play with the interactive application you can get images like these:

With more and more faces this polyhedron is more and more like a sphere:


One way to construct a polyhedron inside a sphere is as follows:
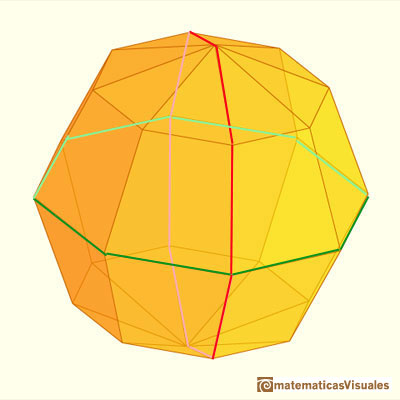
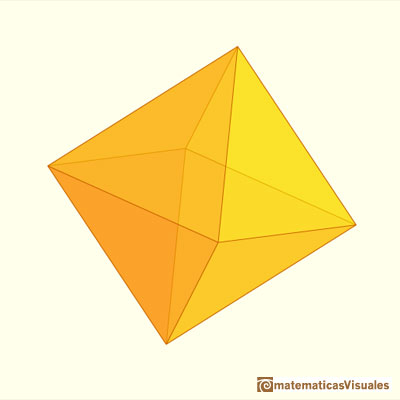
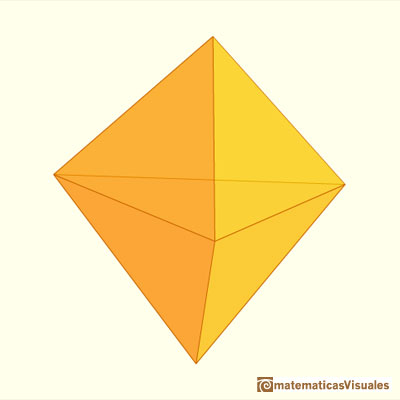
Consider a sphere and let N and S be the North ans South poles of this sphere and let C be its equatorial circle. Inscribe in C a regular polygon with a number of sides which is a multiple of 4, say 4n. Then construct 2n 4n-gons, each of which has a vertex at N, another at S and two vertices passing through two opposite corners of the equatorial polygon (like longitude lines). Then connect the vertices of these polygons with 'latitude lines'. The result is a polyhedron with 8n^2 faces.
If n=1 the result is the octahedron.

If n=2 the result is a polyhedron with 32 faces.



If n=3 the result is a polyhedron with 72 faces, that was known as Campanus' sphere and Luca Pacioli called it Septuaginta.



Using the interactive application you can draw polyhedra that the polygon in the equatorial circle have an ever or odd number of sides and that the 'longitude polygons' have a different number of sides than the 'equatorial polygon'.


REFERENCES
 NEXT
NEXT
 PREVIOUS
PREVIOUS
MORE LINKS