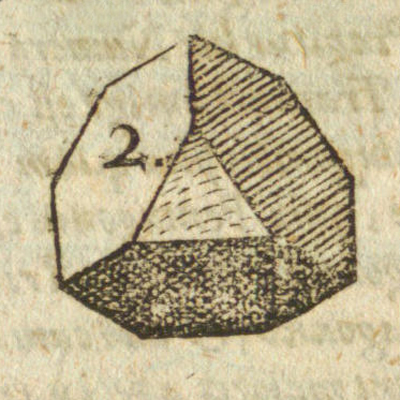
The truncated tetrahedron is an Archimedean polyhedron with four equilateral triangles and four regular hexagons. It was drawn by
Leonardo for Luca Pacioli's book 'De Divina Proportione' and studied by
Kepler in 'Harmonices mundi'.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the truncated tetrahedron.
You can read
Kepler's book 'Harmonices Mundi' in Posner Library Collection.
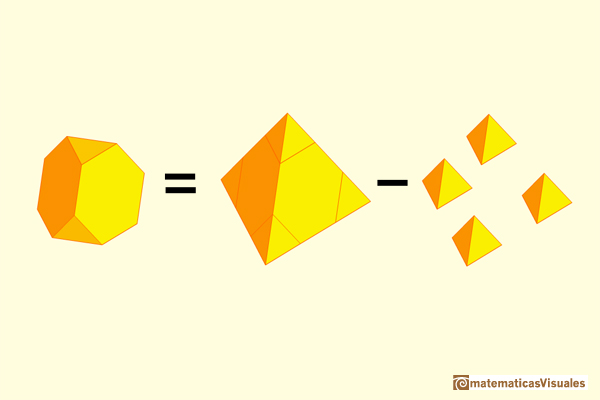
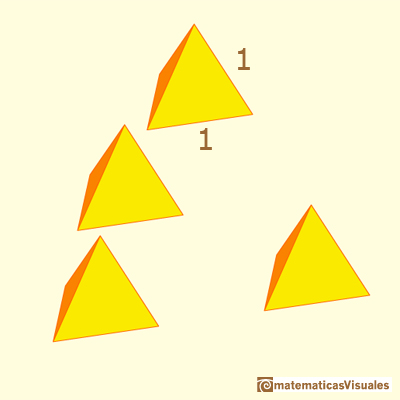
We know how to calculate the volume of a tetrahedron. To calculate the volume of a truncated tetrahedron the main idea is:
We want to calculate the volume of a truncated tetrahedron of side length 1. We can consider a tetrahedron of side length 3.
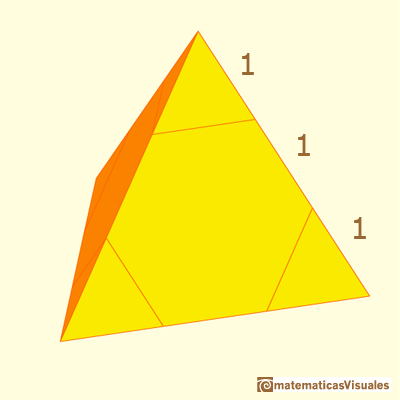
We need to remember that the volume of a tetrahedron of side length a is:
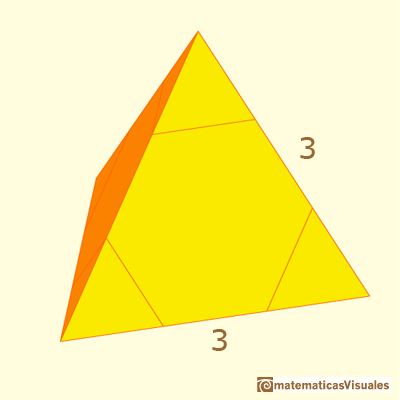
Then we start with a tetrahedron of side length 3. Its volume is:
Now we need the volume of a tetrahedron of side length 1:
The volume of a truncated tetrahedron of side lenght 1 is:
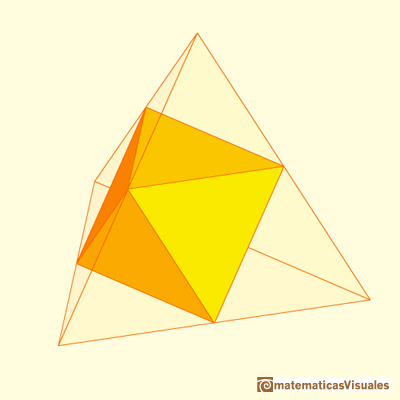
You can control how deep is the truncation:
You get the octahedron as an extreme case:
You can play with transparency to get beautiful projections:
REFERENCES
W.W. Rouse Ball and H.S.M. Coxeter - 'Matematical Recreations & Essays', The MacMillan Company, 1947.
Magnus Wenninger - 'Polyhedron Models', Cambridge University Press.
Peter R. Cromwell - 'Polyhedra', Cambridge University Press, 1999.
MORE LINKS

A very simple technique to build complex and colorful polyhedra.

The volume of a tetrahedron is one third of the prism that contains it.

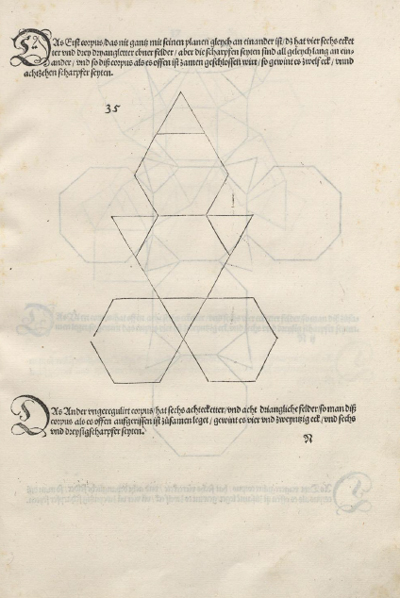
The first drawing of a plane net of a regular tetrahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .

The volume of an octahedron is four times the volume of a tetrahedron. It is easy to calculate and then we can get the volume of a tetrahedron.

Some properties of this platonic solid and how it is related to the golden ratio. Constructing dodecahedra using different techniques.
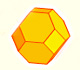
The truncated octahedron is an Archimedean solid. It has 8 regular hexagonal faces and 6 square faces. Its volume can be calculated knowing the volume of an octahedron.

The stellated octahedron was drawn by Leonardo for Luca Pacioli's book 'De Divina Proportione'. A hundred years later, Kepler named it stella octangula.

A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of a cube.

A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of an octahedron.

The twelve vertices of an icosahedron lie in three golden rectangles. Then we can calculate the volume of an icosahedron
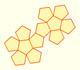
The first drawing of a plane net of a regular dodecahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .
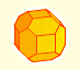
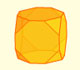
You can chamfer a cube and then you get a polyhedron similar (but not equal) to a truncated octahedron. You can get also a rhombic dodecahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the truncated octahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the cuboctahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the stellated octahedron (stella octangula).

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the dodecahedron.

These polyhedra pack together to fill space, forming a 3 dimensional space tessellation or tilling.

You can chamfer a cube and then you get a polyhedron similar (but not equal) to a truncated octahedron. You can get also a rhombic dodecahedron.

Modular Origami is a nice technique to build polyhedra.

Examples of polyhedra built using tensegrity.

Examples of polyhedra built using tubes.

Examples of polyhedra built using Zome.













 NEXT
NEXT
 PREVIOUS
PREVIOUS