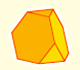
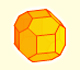
|
|
|
The Truncated Octahedron is a space filling polyhedron
The truncated octahedron is an Archimedean solid. It has 8 regular hexagonal faces and 6 square faces.
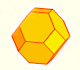
The truncated octahedron is an Archimedean solid. It has 8 regular hexagonal faces and 6 square faces. Its volume can be calculated knowing the volume of an octahedron.
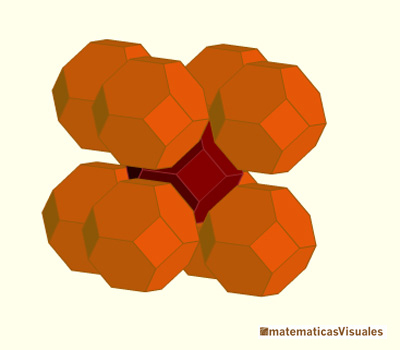
It is a space-filling polyhedron. These polyhedra pack together to fill space, forming a 3 dimensional space tessellation or tilling.
Using eight half cubes we can make a truncated octahedron. The cube tesselate the space an so do the truncated octahedron. We can calculate the volume of a truncated octahedron.
Steinhaus, in his book 'Mathematical Snapshots' wrote:[The truncated octahedron] "fills the whole space in such a way that only 4 solids meet in each vertex; it is semiregular -which means that its faces are regular polygons. There is no other solid having these properties and thus it gives the simplest decomposition of space in congruent parts." (pag. 188)
REFERENCES
Hugo Steinhaus, Mathematical Snapshots, Dover Publications (third edition, 1999)
We can read some pages of this book in Google Books:
Mathematical Snapshots by Hugo Steinhaus.
Magnus Wenninger - 'Polyhedron Models', Cambridge University Press.
Peter R. Cromwell - 'Polyhedra', Cambridge University Press, 1999.
H.Martin Cundy and A.P. Rollet, 'Mathematical Models', Oxford University Press, Second Edition, 1961.
NEXT
The truncated octahedron is an Archimedean solid. It has 8 regular hexagonal faces and 6 square faces. Its volume can be calculated knowing the volume of an octahedron.
PREVIOUS
Using eight half cubes we can make a truncated octahedron. The cube tesselate the space an so do the truncated octahedron. We can calculate the volume of a truncated octahedron.
MORE LINKS
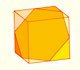
We can cut in half a cube by a plane and get a section that is a regular hexagon. Using eight of this pieces we can made a truncated octahedron.
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the truncated octahedron.
The volume of an octahedron is four times the volume of a tetrahedron. It is easy to calculate and then we can get the volume of a tetrahedron.
The volume of a tetrahedron is one third of the prism that contains it.
The first drawing of a plane net of a regular tetrahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .
Some properties of this platonic solid and how it is related to the golden ratio. Constructing dodecahedra using different techniques.
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the cuboctahedron.
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the dodecahedron.
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the stellated octahedron (stella octangula).
The stellated octahedron was drawn by Leonardo for Luca Pacioli's book 'De Divina Proportione'. A hundred years later, Kepler named it stella octangula.
The compound polyhedron of a cube and an octahedron is an stellated cuboctahedron.It is the same to say that the cuboctahedron is the solid common to the cube and the octahedron in this polyhedron.
The truncated tetrahedron is an Archimedean solid made by 4 triangles and 4 hexagons.
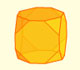
When you truncate a cube you get a truncated cube and a cuboctahedron. If you truncate an octahedron you get a truncated octahedron and a cuboctahedron.
You can chamfer a cube and then you get a polyhedron similar (but not equal) to a truncated octahedron. You can get also a rhombic dodecahedron.