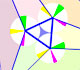
|
|
|
Lines of Simson-Wallace
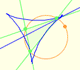
We can start with a triangle and its circunscribed circle. If P is any point belonging to this circuncircle:
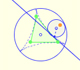
Then we can consider the feet of the perpendiculars from P to the three sides of the triangle (these are ortogonal projections of a point onto the sides or their prolongations):
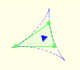
These three feet of the perpendiculars lie on a line:
This line is called the Simson Line of P respect to the triangle or Wallace-Simson Line. The first to mention this line was Wallace (1768-1843), in 1799, thirty years after Simson's death (1687-1768).
REFERENCES
Coxeter, H. S. M. Introduction to Geometry, 2nd ed. New York: John Wiley and sons, 1969.
Coxeter, H. S. M. and Greitzer, S. L. Geometry Revisited. Washington, DC: Math. Assoc. Amer.
de Guzmán, Miguel 'The envelope of the Wallace-Simson lines of a triangle. A simple proof of the Steiner theorem on the deltoid'.
RACSAM, vol. 95, 2001.
Dörrie, H. 100 Great Problems of Elementary Mathematics: Their History and Solutions. New York: Dover, 1965.
NEXT
MORE LINKS
Steiner deltoid is a hypocycloid related with the nine point circle of a triangle.
Central angle in a circle is twice the angle inscribed in the circle.
Interactive 'Mostation' of the property of central and inscribed angles in a circle. Case I: When the arc is half a circle the inscribed angle is a right angle.
Interactive 'Mostation' of the property of central and inscribed angles in a circle. Case II: When one chord that forms the inscribed angle is a diameter.
Interactive 'Mostation' of the property of central and inscribed angles in a circle. The general case is proved.
Using a ruler and a compass we can draw fifteen degrees angles. These are basic examples of the central and inscribed in a circle angles property.
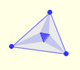
The three points of intersection of the adjacent trisectors of the angles of any triangle are the vertices of an equilateral triangle (Morley's triangle)
Interactive animation about John Conway's beautiful proof of Morley's Theorem