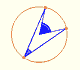
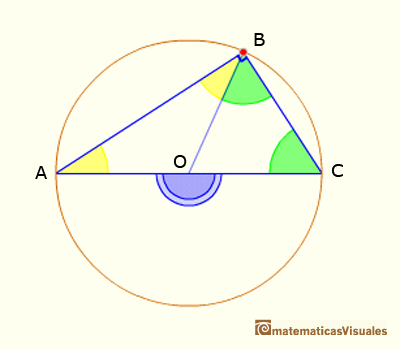
Central angle in a circle is twice the angle inscribed in the circle.
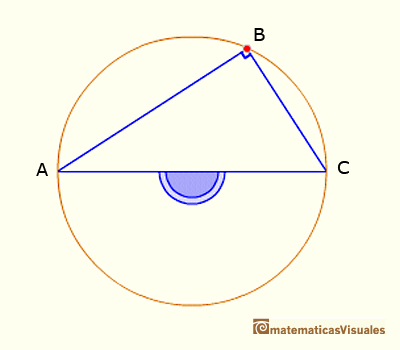
CASE 1. Every inscribed angle that subtends a diameter is a right angle.
This is a particular case of the Central Angle Theorem because the central angle is now 180º.
We want to probe that
The base of these results is "pons asinorum", that is to say,
that the angles of the base of an isosceles triangle are equal.
Adding the angles of the triangle ABC we can write:
Dividing by two:
This ends the demostration of Case I. The next case is when one of the chords that forms the inscribed angle is a diameter.
You can see an interactive demostration of Central and inscribed angles in a circle |Case II.
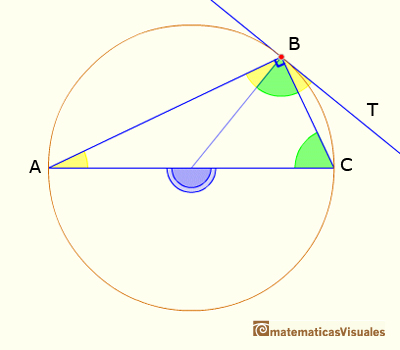
Now we can probe a particular case of Proposition III.32 (about the angle between a tangent and a secant):
MORE LINKS
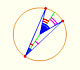
Interactive 'Mostation' of the property of central and inscribed angles in a circle. The general case is proved.
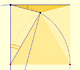
Using a ruler and a compass we can draw fifteen degrees angles. These are basic examples of the central and inscribed in a circle angles property.

Demonstration of Pythagoras Theorem inspired in Euclid.
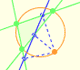
Each point in the circle circunscribed to a triangle give us a line (Wallace-Simson line)

Interactive demonstration of the Wallace-Simson line.
You can draw a regular pentagon given one of its sides constructing the golden ratio with ruler and compass.
In his book 'Underweysung der Messung' Durer draw a non-regular pentagon with ruler and a fixed compass. It is a simple construction and a very good approximation of a regular pentagon.

The diagonal of a regular pentagon are in golden ratio to its sides and the point of intersection of two diagonals of a regular pentagon are said to divide each other in the golden ratio or 'in extreme and mean ratio'.

 NEXT
NEXT



















 PREVIOUS
PREVIOUS



