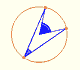
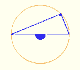
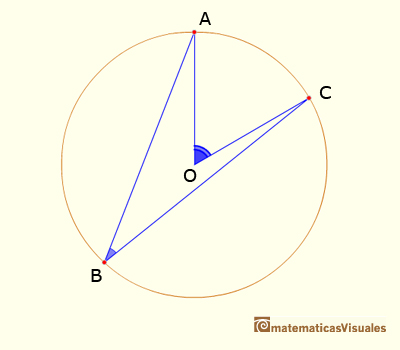
Central and Inscribed Angle in a Circle: Case III
The general case of the Central Angle Theorem can be proved using the previous case. To do that we can draw the diameter that pases through the vertex of the inscribed angle. Then, depending on the position of the points, it is enough to add or to subtract some angles.
In this position we have to add two central angles (and we use Case II):
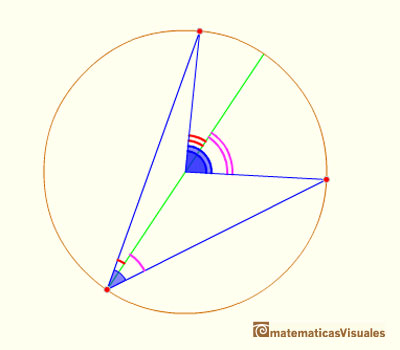
In this position we have to substract two central angles (and we use Case II):
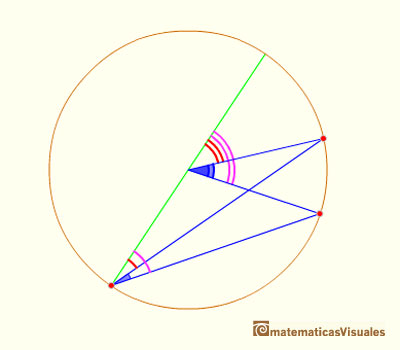
With Case I, Case II and this General Case we have finished the demostration of the Central Angle Theorem.
REFERENCES
Euclides, The Elements
 NEXT
NEXT
 PREVIOUS
PREVIOUS
MORE LINKS
Using a ruler and a compass we can draw fifteen degrees angles. These are basic examples of the central and inscribed in a circle angles property.
You can draw a regular pentagon given one of its sides constructing the golden ratio with ruler and compass.
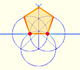
In his book 'Underweysung der Messung' Durer draw a non-regular pentagon with ruler and a fixed compass. It is a simple construction and a very good approximation of a regular pentagon.