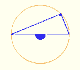
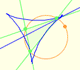
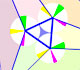
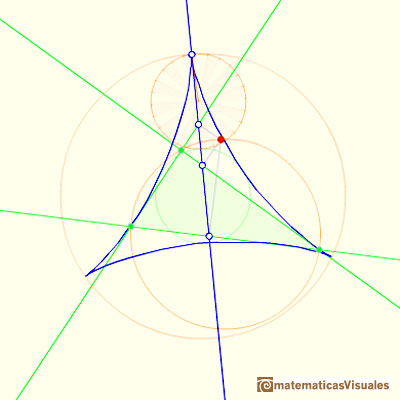
We know that Jacob Steiner (1796-1863) proved that the envelope of the Wallace-Simson lines is a curve that has three cuspidal points that is called the Steiner deltoid.

Steiner deltoid

The Simson-Wallace lines of a triangle envelops a curve called the Steiner Deltoid.

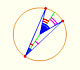
And a deltoid is one specific curve in the family of hypocycloid curves. A hypocycloid is a plane curve generated by the trace of a fixed point on a small circle that rolls without slipping within a larger circle. A deltoid is a hypocycloid in which the inner turning circle has a radius that is one third the radius of the outer circle.

In this page we explore the fact that the Steiner Deltoid is a hypocycloid. It is to say that it is generated by a circle rolling inside another circle.

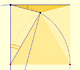
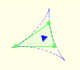
Both circles are related with the Feuerbach circle or the nine-point circle, (green circle in the image). The radius of the nine-point circle is half the radius of the circumscribed circle. The exterior circle has the same center as the nine-point circle and its radius is three times the radius of the nine-point circle.

The rolling circle has the same radius as the Feuerbach circle and both are tangent.

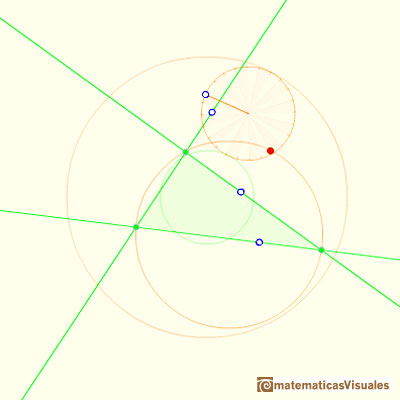
When the small circle rolls without slipping generates the Steiner deltoid.

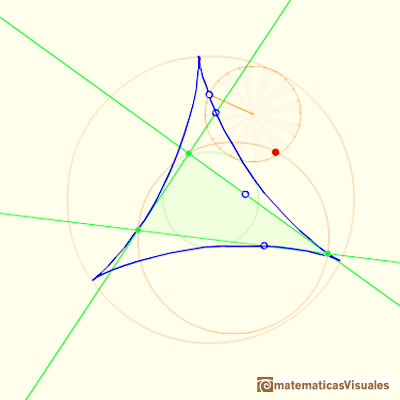
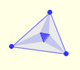
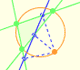
The Steiner deltoid is tangent to the nine-point circle.

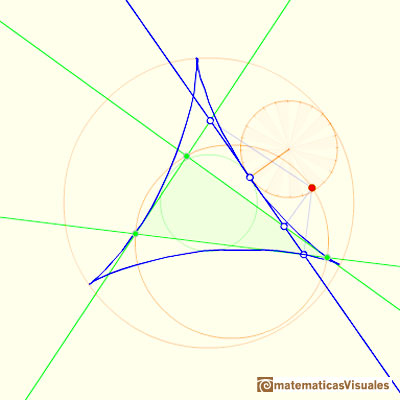
The three tangents to the deltoid at the three cuspides pass through the center of the Feuerbach circle.

MORE LINKS

Wallace-Simson lines

Each point in the circle circunscribed to a triangle give us a line (Wallace-Simson line)

Wallace-Simson lines | Demonstration

Interactive demonstration of the Wallace-Simson line.

Central and inscribed angles in a circle

Central angle in a circle is twice the angle inscribed in the circle.

Central and inscribed angles in a circle | Mostration | Case I

Interactive 'Mostation' of the property of central and inscribed angles in a circle. Case I: When the arc is half a circle the inscribed angle is a right angle.

Central and inscribed angles in a circle | Mostration | Case II

Interactive 'Mostation' of the property of central and inscribed angles in a circle. Case II: When one chord that forms the inscribed angle is a diameter.

Central and inscribed angles in a circle | Mostration | General Case

Interactive 'Mostation' of the property of central and inscribed angles in a circle. The general case is proved.

Drawing fifteen degrees angles

Using a ruler and a compass we can draw fifteen degrees angles. These are basic examples of the central and inscribed in a circle angles property.

Morley Theorem

The three points of intersection of the adjacent trisectors of the angles of any triangle are the vertices of an equilateral triangle (Morley's triangle)

John Conway's proof of Morley's Theorem

Interactive animation about John Conway's beautiful proof of Morley's Theorem