In the following video you can see the main idea of this page: [TO DO: Audio in English or subtitles]
We already know that Pappus of Alexandria (around the year 320) was interested in the shape of honeycombs. He thought that the hexagonal prism was an optimal solution for the bees. It is to say that this hexagonal structure minimized the amount of wax that the bees needed to build the cells. These cells contain more honey in relation with the surface area.

Pappus wrote:
Bees, then, know just this fact which is of service to themselves, that the hexagon is greater than the square and the triangle and will hold more honey for the same expenditure of material used in constructing the different figures. (You can read more about Pappus in note 16 of the book 'The Six Cornered Snowflake' or in Sir Thomas Heath's book 'A History of Greek Mathematics' [Dover, 1981]).
Pappus considered only the hexagonal prism but not the rhombic bottom.
The problem that a hexagonal prism is optimal or isoperimetric was known as the Honeycomb Conjeture. This conjeture remainded unproven until the middle of the twentieth century (Laszlo Fejes Toth, Thomas Hale). And Toth proved that the bases of the cells are not optimal shapes.
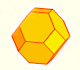
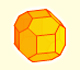
After Kepler's discovery of the Rhombic Dodecahedron looking at the bottom of bee cells, other mathematicians and scientits were interested in studying how the bees build the bottom of their cells.
Maraldi, in 1712, was able to decided the measure of the angles of the rhombic faces of the bottom of the cell (the obtuse one is now called Maraldi angle).

During the 18th century interest turned to the optimization problem of choosig the rhombi at the bottom of the cells so as to make the area of the cells as small as possible.
The French entomologist Réaumur posed the problem to Samuel Koening, a young Swiss mathematician: Given an hexagonal cell terminated by three similar and equal rhombi, what is the configuration which requires the least quantity of material for its construction?
In 1739, Koening wrote a letter to Réaumur and his answer was very similar to Maraldi's. This letter was unpublished and is lost. We do not know how Koening studied this problem.
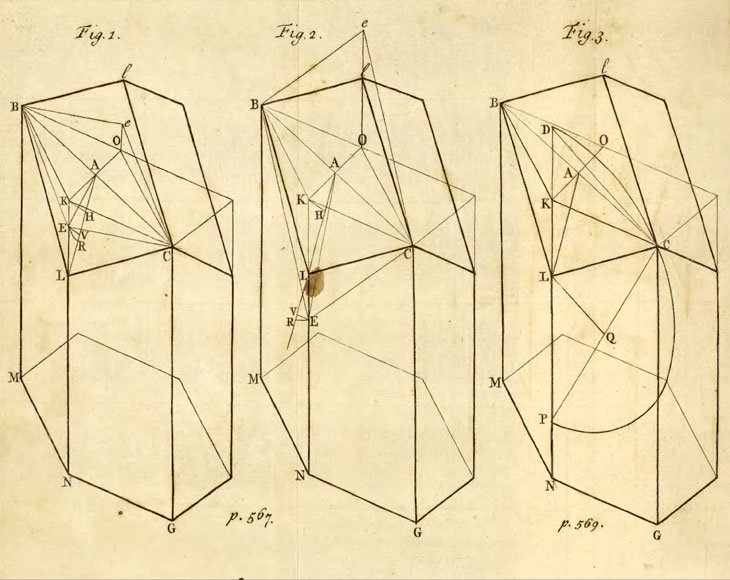
A few years later, in 1743, the Scottish mathematician Colin Maclaurin (1698-1746) wrote 'On the Bases of the Cells wherein the Bees deposite their Honey'. There he solved the problem.
In this page we are going to study this optimization problem: We want to close a hexagonal prism as bees do, using three equal rhombi.
Then, which is the shape of these three rhombi that closes the hexagonal prism with the minimum surface area?
You can play with the applet to see different ways to do that. Changing the height of the cell we change the amount of wax needed to close the cell.
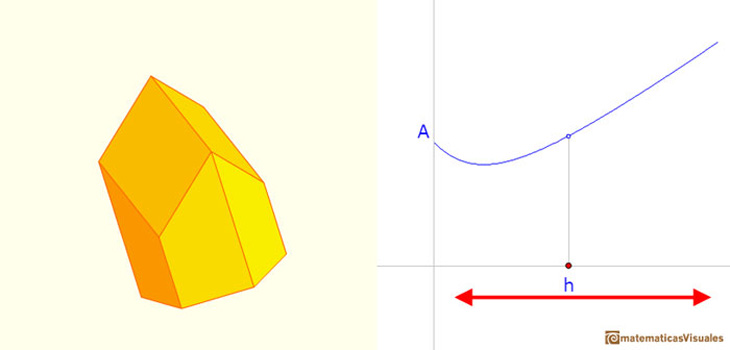
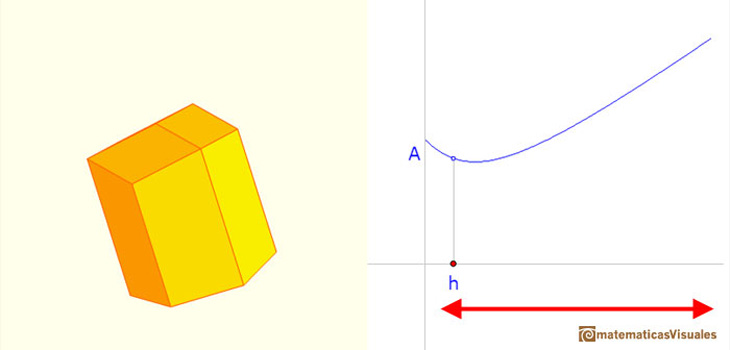
If the shape changes the surface area is different.


We want to minimize this surface area.
We can notice that the volume of these different cells is always the same.
You can play with the applet, opening and closing the keel, to see the reason:
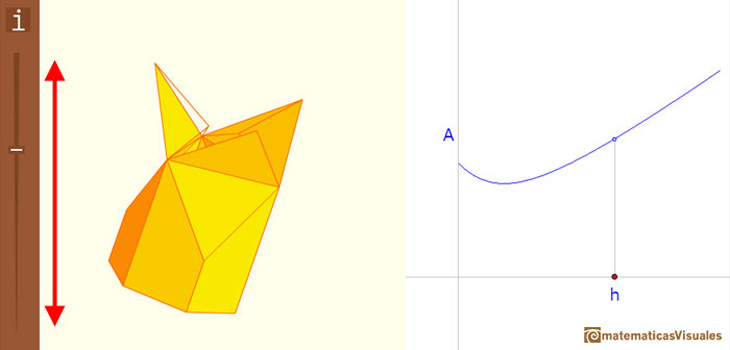
To close the cell we cut three pyramids from the hexagonal prism and then we put these three pyramids together to form the keel, then the volume is always the same.


The surface area needed to close the prism changes when we change the shape.
We can calculate the lateral hexagonal prims surface area but we will not need this calculation. Our problem does not depend on the height of the prism and we can suppose that it is large enough. Our problem is related with the three rhombi that close the prism, and we want to optimize this surface area.
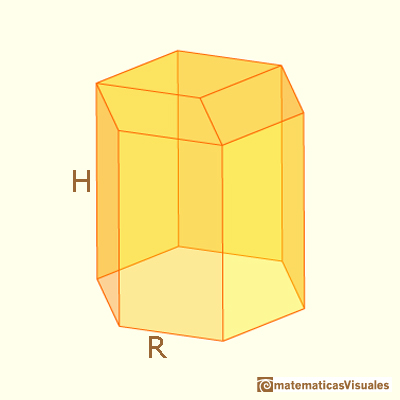
R is the radius of the circumcircle of the hexagon and h is the height to the rhombus vertex from one vertex of the hexagon. h is our independen variable. Changing h we change the shape and the surface area needed to close the prism (but no the volume of the body).
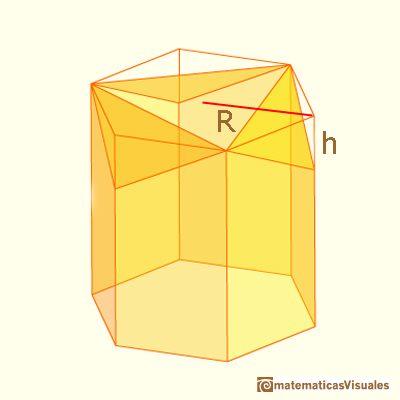
We can make our calculations considering only one rhombus because the three of them are equal.
If we start with the hexagonal prism lateral surface area the first thing that we can do is to cut two right triangles. These triangles t have base R and height h.
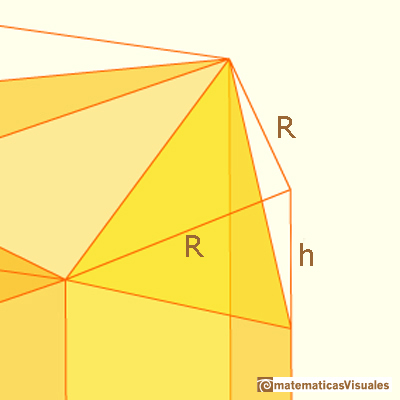
Then the area of one of these triangles t is:
To close the prism we add one rhombus made of two triangles r. They have base d and height a.
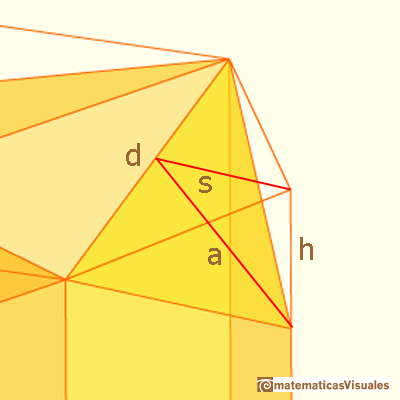
The diagonal d is easy to calculate, because it is one diagonal of the hexagon:
We need s that is related with R, the radius of the circumcircle:
Now we can apply the Phytagorean Theorem to calculate a:
Then the surface area of the triangle r is:
We can simplify a little:
The surface area of the rhombus that we add is twice the area of this triangle.
Now we can calculate the surface area of our body. Taking into consideration only one rhombus, we cut two triangles t and we add two triangles r.
The function that we want to optimize is:
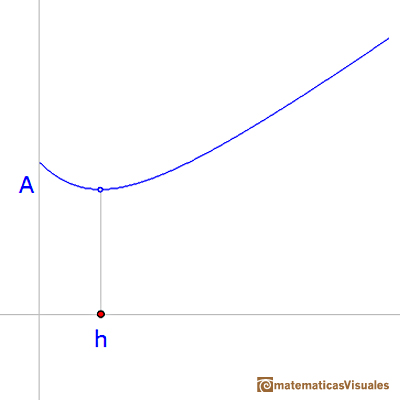
To obtain the minimun of this function we can use the derivative:
Then the minimum is:
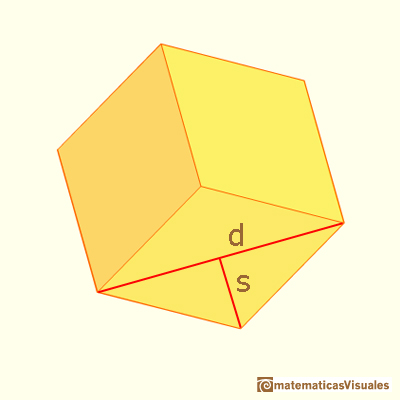
We can check the relation between the two diagonals of this rhombus:
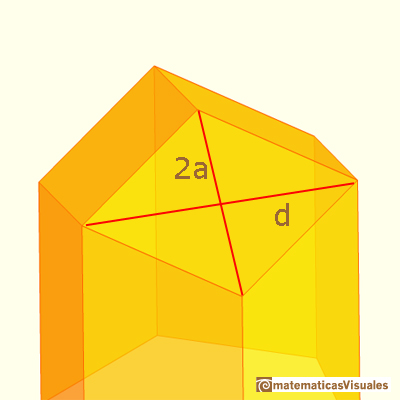
This rhombus is a very special one. With twelve of these rhombi we can build a polyhedra called rhombic dodecahedron.
Johannes Kepler was the first mathematician who wrote about the rhombic dodecahedron and thought that bees close their cells with rhombi that are rhombi of a rhombic dodecahedron.

Another video with a bee cell:
The following drawing is from Colin Maclaurin's letter 'On the Bases of the Cells wherein the Bees deposite their Honey'.

But this closing of the bee cells are really optimal? László Fejes Tóth wrote the article 'What the bees know and what they do not know' in 1964. There he proposed a better clousure of the bee cells. He wrote:
Instead of closing the bottom of a cell by three rhombi, as the bees do, it is always more efficient to use two hexagons and two rhombi.
This is a drawing from this article:
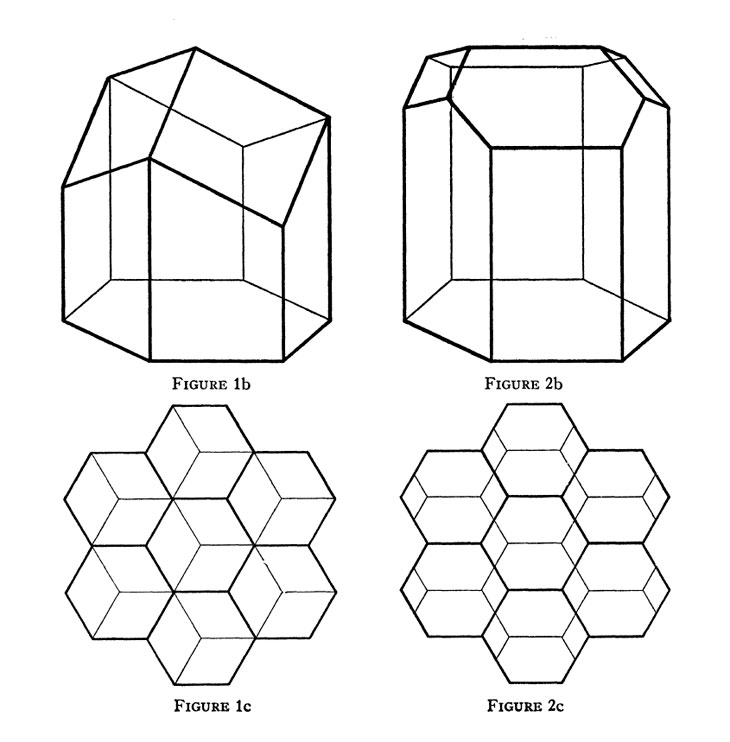
Fejes Tóth concluded:
We must admit that all this has no practical consequence. By building such cells the bees would save per cell less than 0.35% of the area of a an opening (and a much smaller percentage of the surface-area of a cell). On the other hand, the walls of the bee-cells have a non-negligible width which is, in addition, far from being uniform and even the openings of the bee-cells are far from being exactly regular. Besides, the building style of the bees is definitely simpler than that described above. So we would fail in shaking someone's conviction that the bees have a deep geometrical intuition.
Can we explore how bees actually build their cells?
This is not an easy task. This is because beekeepers help bees placing a wax sheet with rhombi in each frame of a beehive. Then bees have less work to do to build their cells (to produce wax is a very costly work).
Then we need to find a wild beehive where bees are building their cells in a natural way, without human intervention.
I could do this thanks to my friend Luis Larriba. He is a ceramist, expert in historical pottery and a keen beekeeper. Together we went to a place near Tartanedo (a small town in Guadalajara, Spain) to see how bees work in a natural environment.
There I could collect a natural honeycomb. I carefully destroyed the hexagonal prisms to see the bottom of several cells.
The conclusion is clear: we can see some of the bottom of these cells that are made of three rhombi almost perfect. But others are different and we can see that are made of two hexagons and two rhombi.

REFERENCES
 NEXT
NEXT
 PREVIOUS
PREVIOUS
MORE LINKS