The Rhombic Dodecahedron and the cube
|
|
|
A rhombic dodecahedron could be made by a cube and six pyramids. Then it is easy to calculate the volumen of this polyhedron.
You can build a Rhombic Dodecahedron adding six pyramids to a cube. This fact has several interesting consequences.
And we know that the rhombic dodecahedron is a space-filling polyhedron.
The Rhombic Dodecahedron fills the space without gaps.
In this page we are going to see from another point of view the relation between the cube and the rhombic dodecahedron.
You can put these six pyramids in a chain like this:
Cundy and Rollet wrote: "The resulting chain of pyramids can be turned inwards to form a cube, or, turned outwards, placed as a jacket over another cube to form the rhombic dodecahedron." (Cundy and Rollet, pag. 122.)
Turning inwards you get a cube:
This is a model made by cardboard:
We already know that there is a relation between the Din A paper size and the rhombic dodecahedron.
Adding six pyramids to a cube you can build new polyhedra with twenty four triangular faces. For specific pyramids you get a Rhombic Dodecahedron that has twelve rhombic faces.
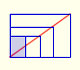
There is a standarization of the size of the paper that is called DIN A. Successive paper sizes in the series A1, A2, A3, A4, and so forth, are defined by halving the preceding paper size along the larger dimension.
Michael Grodzins has explored the possibilities of folding dipyramids using Din A paper size. Then he link six of these dipyramids and he build a rhombic dodecahedron. He published several pages about that: Instructables: (Un)Folding the Mysteries of A4 Paper, Instructables: Mysteries of the (Di)pyramids and more.
This is my model, following his instructions:
REFERENCES
Johannes Kepler - The Six Cornered Snowflake: a New Year's gif - Paul Dry Books, Philadelphia, Pennsylvania, 2010. English translation of Kepler's book 'De Nive Sexangula'.
With notes by Owen Gingerich and Guillermo Bleichmar and illustrations by the spanish mathematician Capi Corrales Rodrigáñez.
D'Arcy Thompson - On Growth And Form - Cambridge University Press, 1942.
Hugo Steinhaus - Mathematical Snapshots - Oxford University Press - Third Edition.
Magnus Wenninger - 'Polyhedron Models', Cambridge University Press.
Peter R. Cromwell - 'Polyhedra', Cambridge University Press, 1999.
H.Martin Cundy and A.P. Rollet, 'Mathematical Models', Oxford University Press, Second Edition, 1961.
W.W. Rouse Ball and H.S.M. Coxeter - 'Matematical Recreations & Essays', The MacMillan Company, 1947.
NEXT
Starting with a Rhombicubotahedron we can add pyramids over each face. The we get a beautiful polyhedron that it is like a star.
PREVIOUS
The Rhombic Dodecahedron fills the space without gaps.
MORE LINKS
Humankind has always been fascinated by how bees build their honeycombs. Kepler related honeycombs with a polyhedron called Rhombic Dodecahedron.
We want to close a hexagonal prism as bees do, using three rhombi. Then, which is the shape of these three rhombi that closes the prism with the minimum surface area?.
Adding six pyramids to a cube you can build new polyhedra with twenty four triangular faces. For specific pyramids you get a Rhombic Dodecahedron that has twelve rhombic faces.
You can build a Rhombic Dodecahedron adding six pyramids to a cube. This fact has several interesting consequences.
The obtuse angle of a rhombic face of a Rhombic Dodecahedron is known as Maraldi angle. We need only basic trigonometry to calculate it.
There are two essential different ways to pack spheres in an optimal disposition. One is related with the Rhombic Dodecaedron and the other to a polyhedron called Trapezo-rombic dodecahedron..
Using a basic knowledge about the Rhombic Dodecahedron, it is easy to calculate the density of the optimal packing of spheres.
Tetraxis is a wonderful puzzle designed by Jane and John Kostick. We study some properties of this puzzle and its relations with the rhombic dodecahedron. We can build this puzzle using cardboard and magnets or using a 3D printer.
There is a standarization of the size of the paper that is called DIN A. Successive paper sizes in the series A1, A2, A3, A4, and so forth, are defined by halving the preceding paper size along the larger dimension.
Material for a session about polyhedra (Zaragoza, 9th May 2014). Simple techniques to build polyhedra like the tetrahedron, octahedron, the cuboctahedron and the rhombic dodecahedron. We can build a box that is a rhombic dodecahedron.
A Cube can be inscribed in a Dodecahedron. A Dodecahedron can be seen as a cube with six 'roofs'. You can fold a dodecahedron into a cube.
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the augmented rhombicuboctahedron.
We can see the interior of the augmented rhombicuboctahedron. Luca Pacioli wrote that you 'can see the interior only with your imagination'.
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the truncated octahedron.
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the cuboctahedron.
A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of a cube.
A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of an octahedron.
The volume of an octahedron is four times the volume of a tetrahedron. It is easy to calculate and then we can get the volume of a tetrahedron.
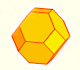
The truncated octahedron is an Archimedean solid. It has 8 regular hexagonal faces and 6 square faces. Its volume can be calculated knowing the volume of an octahedron.
These polyhedra pack together to fill space, forming a 3 dimensional space tessellation or tilling.
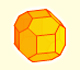
You can chamfer a cube and then you get a polyhedron similar (but not equal) to a truncated octahedron. You can get also a rhombic dodecahedron.
If you fold the six roofs of a regular dodecahedron into a cube there is an empty space. This space can be filled with an irregular dodecahedron composed of identical irregular pentagons (a kind of pyritohedron).