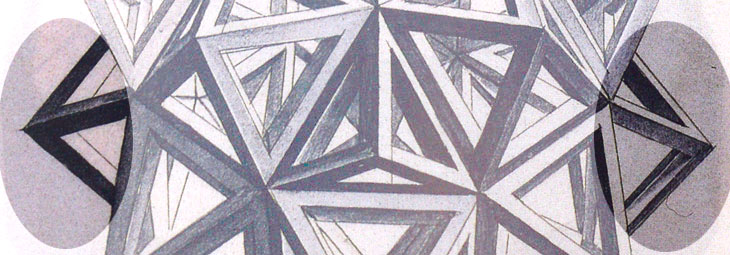
This video is an adaptation of the drawing that Leonardo da Vinci made of the augmented rhombicuboctahedron
(Vigintisex basium elevatus) for Luca Pacioli's book 'De Divina Proportione'.
The process of adding pryramids to a polyhedron is called 'augmentation'.
We have already used this technique when we study the rhombicdodecahedron as an augmented cube:

Adding six pyramids to a cube you can build new polyhedra with twenty four triangular faces. For specific pyramids you get a Rhombic Dodecahedron that has twelve rhombic faces.
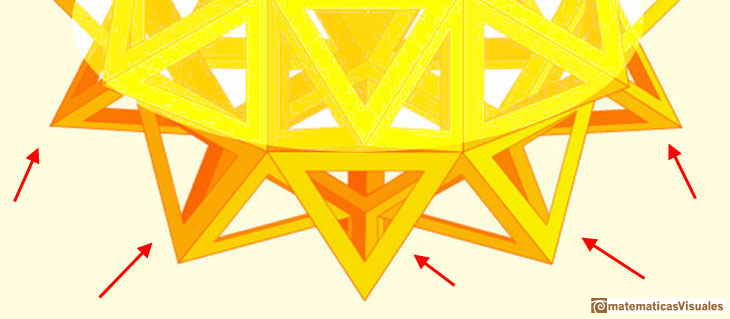
In this page we are going to study the augmented rhombicuboctahedron.
The rhombicuboctahedron was also discribed by Luca Pacioli and was drawn by Leonardo:

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the rhombicuboctahedron.
Pacioli wrote about this 'elevatus' or augmented polyhedron (Spanish translation):
"El cuerpo de veintiséis bases sólido o hueco elevado recibe en su formación ciento cuarenta y cuatro líneas que, unidas entre sí,
según las oportunas exigencias, originan en él doscientos ochenta y ocho ángulos superficiales y veintiséis sólidos elevados
piramidales, dieciocho de los cuales son deterinados por cuatro ángulos agudos superficiales y ocho por tres agudos. Está
compuesto dicho cuerpo por veintiséis pirámides lateradas, dieciocho de las cuales son cuadrangulares y ocho triangulares,
que se pueden discernir por la vista en el exterior, y por el mencionado cuerpo de veintiséis bases sólido plano, interior,
que solamente puede ser captado por la imaginación. Sus veintiséis bases son igualmente bases de las antes mencionadas
veintiséis pirámides, es decir, las dieciocho cuadrangulares de las dieciocho pirámides cuadrangulares y las ocho triangulares
de las ocho pirámides cuadrangulares."
('La divina proporción' de Luca Pacioli, page 98, Spanish translation by Juan Calatrava, Editorial Akal, 4th edition, 2008)
Interacting with the application you can rotate the polyhedron and play with the "hole" in each face:
We can play with a second versión of this interactive application and see the interior of this polyhedron.

We can see the interior of the augmented rhombicuboctahedron. Luca Pacioli wrote that you 'can see the interior only with your imagination'.
We can compare Leonardo da Vinci's drawing with the image generated with the application.
Dutch mathematician and sculptor Rinus Roelofs pointed out an error in da Vinci's drawing.
Dirk Huylebrouck wrote an article that was published in Scientific American magazine about this mistake:
Lost in Triangulation: Leonardo da Vinci's Mathematical Slip-Up,
Leonardo da Vinci was a genius, his drawings for Pacioli's book are wonderful and this is only an anecdote that alow us to study and enjoy this beautiful polyhedron.
The apexes of two triangular pyramids at the bottom left and right seem to be missing.
The main difference is that the pyramid at the bottom should be triangular but it is quadrangular in Leonardo's drawing.
The two pyramids adjacent to it should be quadrangular and symmetric.
A different opinion was published by Carlo H. Sequin. He thinks that Leonardo was depicting an augmented pseudo rhombicuboctahedron rather than an
augmented rhombicuboctahedron.
You can learn more about the pseudo-rhombicuboctahedron following this link:

This polyhedron is also called Elongated Square Gyrobicupola. It is similar to the Rhombicuboctahedron but it is less symmetric.
Then the main problem, the pyramid at the bottom, is now a quadrangular pyramid and Leonardo was right.
We are going to take a look comparing Leonardo's drawing and the augmented pseudo-rhombicuboctahedron. But there is a big objection to this point of
view: if we read Pacioli's book he wrote about several polyhedra in the same order ('planus solidus', 'planus vacuus' 'elevatus solidus' and
'elevatus vacuus'). Then he explained the reader the rhombicuboctahedron ('planus solidus and vacuus') and the augmented rhombicuboctahedron
('evelatus solidus and vacuus') and those are the drawings that we expect from Leonardo.
The next application is an adaptation of Leonardo's drawing but in this case we are using a pseudo-rhombicuboctahedron as
the polyhedron base of the augmentation.
REFERENCES
W.W. Rouse Ball and H.S.M. Coxeter, 'Matematical Recreations & Essays', The MacMillan Company, 1947.
Peter R. Cromwell, 'Polyhedra', Cambridge University Press, 1999.
MORE LINKS

Starting with a Rhombicubotahedron we can add pyramids over each face. The we get a beautiful polyhedron that it is like a star.

This polyhedron is also called Elongated Square Gyrobicupola. It is similar to the Rhombicuboctahedron but it is less symmetric.

Adding six pyramids to a cube you can build new polyhedra with twenty four triangular faces. For specific pyramids you get a Rhombic Dodecahedron that has twelve rhombic faces.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the dodecahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the truncated octahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the cuboctahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the stellated octahedron (stella octangula).

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the octahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the truncated tetrahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the Campanus' sphere.

Adding six pyramids to a cube you can build new polyhedra with twenty four triangular faces. For specific pyramids you get a Rhombic Dodecahedron that has twelve rhombic faces.

You can build a Rhombic Dodecahedron adding six pyramids to a cube. This fact has several interesting consequences.

The first drawing of a plane net of a regular octahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .

Using cardboard you can build beautiful polyhedra cutting polygons and glue them toghether. This is a very simple and effective technique. You can download several templates. Then print, cut and glue: very easy!

A very simple technique to build complex and colorful polyhedra.

Material for a session about polyhedra (Zaragoza, 7th November 2014). We study the octahedron and the tetrahedron and their volumes. The truncated octahedron helps us to this task. We build a cubic box with cardboard and an origami tetrahedron.

Material for a session about polyhedra (Zaragoza, 23rd Octuber 2015) . Building a cube with cardboard and an origami octahedron.

Material for a session about polyhedra (Zaragoza, 13th Abril 2012).

Material for a session about polyhedra (Zaragoza, 9th May 2014). Simple techniques to build polyhedra like the tetrahedron, octahedron, the cuboctahedron and the rhombic dodecahedron. We can build a box that is a rhombic dodecahedron.

The compound polyhedron of a cube and an octahedron is an stellated cuboctahedron.It is the same to say that the cuboctahedron is the solid common to the cube and the octahedron in this polyhedron.
























 NEXT
NEXT
 PREVIOUS
PREVIOUS

































