Pascal's Theorem
Blaise Pascal (1623-1662) was a french mathematician and philosopher.
The theorem that we are going to study here is known as Pascal's Theorem or the Mystic Hexagram.
The nature of this teorem is projective and we can find demonstrations of it in books about Projective Geometry.
In this page we are going to explore this theorem in the Euclidean Plane. This approach has advantages and disadvantages.
Pascal's Theorem: If a hexagon is inscriben in a circle, the three pairs of opposite sides meet in collinear points.
The projective Pascal's Theorem refers to a hexagon inscriben in a conic. From the euclidean point of view we already know that ellipses, parabolas and hyperbolas are conic sections. Then Pascal's Theorem is true in these more general cases. Circles are particular cases of ellipses and the simplest of conic sections. We will see later that this has some disadvantages too.
Then we start with a circle and a hexagon inscribed in it.
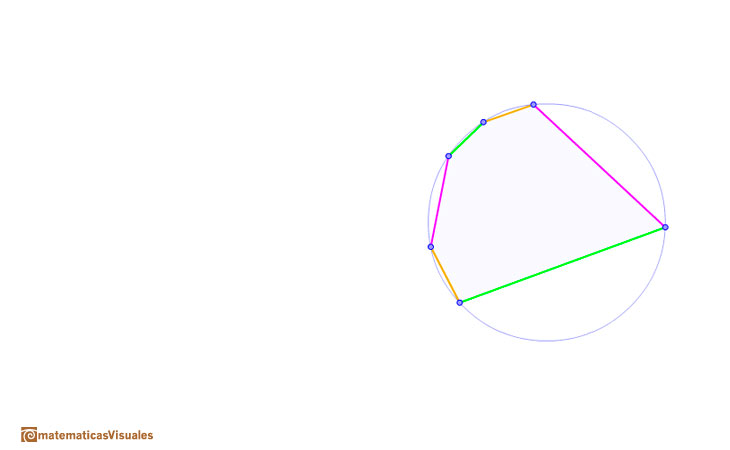
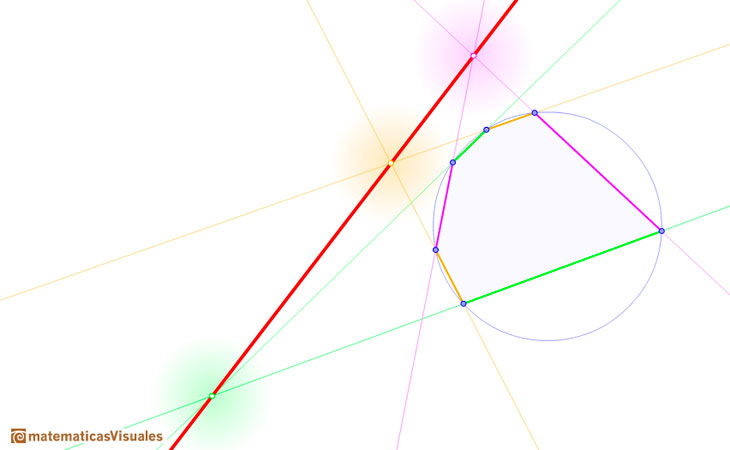
Pairs of opposite sides are drawn using different colors. We can see that they meet in collinear points. This straight line is called Pascal's line.
The hexagon do not need to be a convex one. For example:
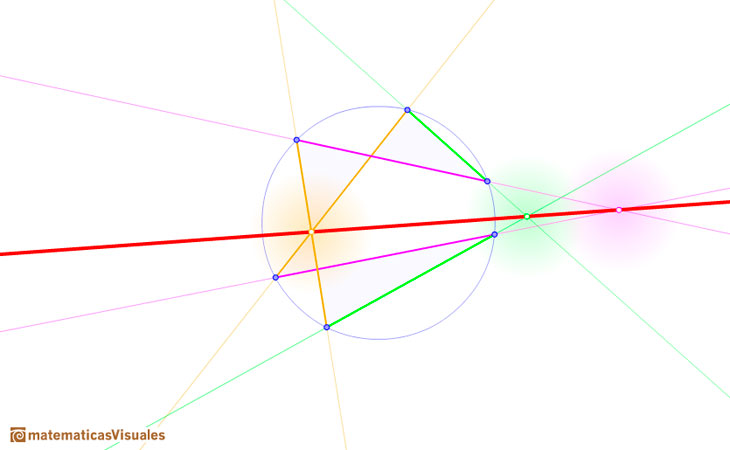
If two points coincide then we consider the side to be the tangent line. The hexagon is now a pentagon.

If two pairs of points coincide then we have a quadrilateral. Then pair of opposite sides and tangents to a pair of opposite vertices intersect on a straight line.

In every triangle inscribed in a circle the sides intersect with the tangents to the opposite vertices on a straight line.
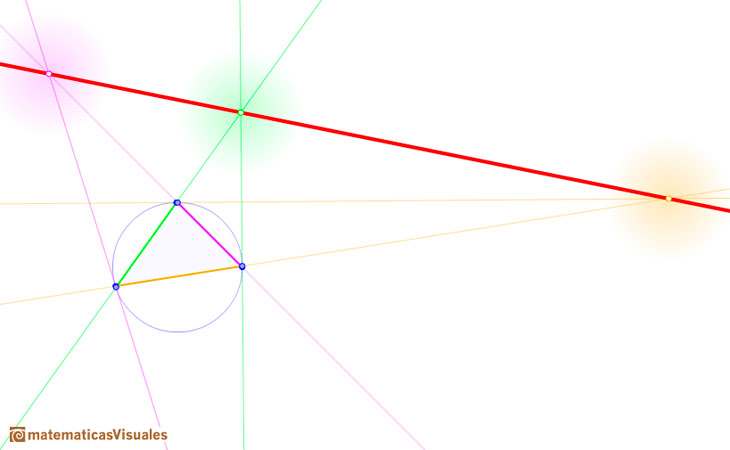
In projective geometry, any two different straight lines meet at one point. When we consider Pascal's Theorem in the Euclidean plane the theorem is also valid but we need to make some adjustement to deal with the special cases when opposite sides are parallel.
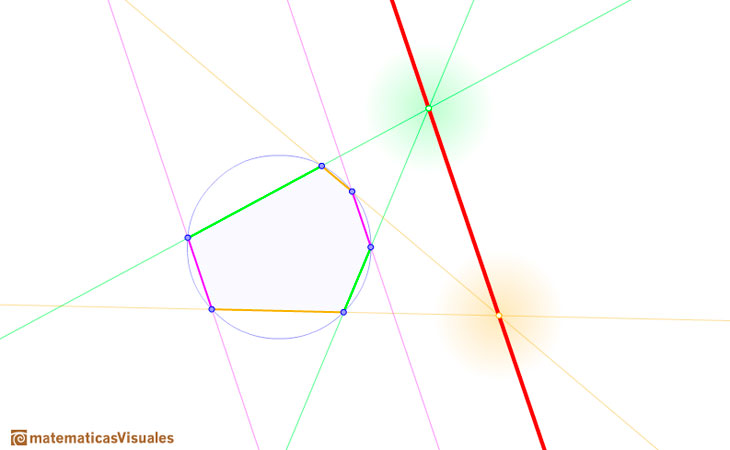
If exactly one pair of opposite sides of the hexagon are parallel then the Pascal line determined by the two points of intersection is parallel to the parallel sides.
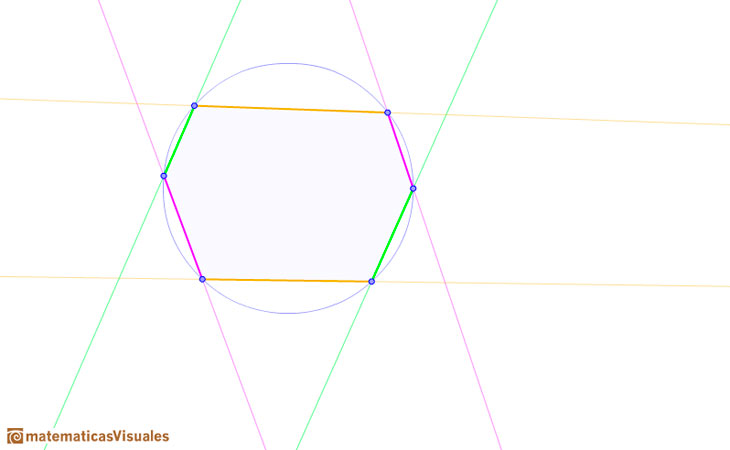
If two pairs of opposite sides of the hexagon are parallel then all three pairs of opposite sides are parallel.
The nature of Pascal's Theorem is projective and we can change the word circle by conic.
Pascal's Theorem: If a hexagon is inscriben in a conic, the three pairs of opposite sides meet in collinear points.
Two stright lines can be considered a degenerate conic. The the theorem it also true in this case. This case is known as theorem of Pappus.
REFERENCES
H.S.M. Coxeter - 'Projective Geometry' - Blaisdell Publishing Company, 1964.
H.S.M. Coxeter - 'The real projective plane', Springer-Verlag, Third edition, 1993.
Howard Eves - 'A Survey of Geometry', Allyn and Bacon, Inc., 1972.
MORE LINKS
Every ellipse has two foci and if we add the distance between a point on the ellipse and these two foci we get a constant.
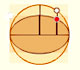
Transforming a circle we can get an ellipse (as Archimedes did to calculate its area). From the equation of a circle we can deduce the equation of an ellipse.

In his book 'On Conoids and Spheroids', Archimedes calculated the area of an ellipse. We can see an intuitive approach to Archimedes' ideas.
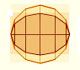
In his book 'On Conoids and Spheroids', Archimedes calculated the area of an ellipse. It si a good example of a rigorous proof using a double reductio ad absurdum.

Transforming a circle we can get an ellipse (as Archimedes did to calculate its area). From the equation of a circle we can deduce the equation of an ellipse.
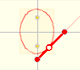
If a straight-line segment is moved in such a way that its extremities travel on two mutually perpendicular straight lines then the midpoint traces out a circle; every other point of the line traces out an ellipse.
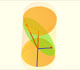
The section of a cylinder by a plane cutting its axis at a single point is an ellipse. A beautiful demonstration uses Dandelin Spheres.

Durer made a mistake when he explanined how to draw ellipses. We can prove, using only basic properties, that the ellipse has not an egg shape .
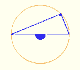
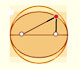
Interactive 'Mostation' of the property of central and inscribed angles in a circle. Case I: When the arc is half a circle the inscribed angle is a right angle.

Interactive 'Mostation' of the property of central and inscribed angles in a circle. Case II: When one chord that forms the inscribed angle is a diameter.
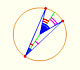
Interactive 'Mostation' of the property of central and inscribed angles in a circle. The general case is proved.













 NEXT
NEXT