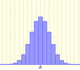
Poisson distribution is discrete (like the binomial) because the values that can take the random variable are natural numbers, although in the Poisson distribution all the possible cases are theoretically infinite.
Poisson distribution is characterized by a single parameter lambda.
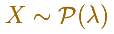
Its density function is given by
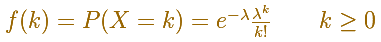
Its mean and variance are the same:
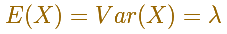
Pfeiffer and Schum wrote in their book "Introduction to Applied Probability":
"This distribution arises in a variety of situations in which it is desired to count the number of occurrences of some phenomenon in an interval of time or space. We suppose that the following conditions hold:
(1) The probability is one that the phenomenon does not occur in an interval of length 0.
(2) The numbers of occurrences in two nonoverlapping intervals are independent.
(3) The probability of a given number of occurrences in an interval depends upon the length of the interval, but not its location.
(4) For small intervals, the probability of exactly one occurrence is very nearly proportional to the length of the interval.
(5) For very small intervals, the probability of more than one occurrence goes to zero faster than the length of the interval.
These assumptions have proven to be reasonable in such diverse applications as:
1. Certain studies of traffic patterns the number of cars past a given point in time interval of length t.
2. The number of calls on a telephone switchboard in time interval t.
3. The number of failures of a complicated system in time interval t.
4. The number of items of a given type of merchandise sold in a time period of length t.
5. The number of suicides in a time interval t.
6. The number of bacteria in a specified volume t of liquid.
7. The number of industrial accidents in a time interval t".
[Pfeiffer and Schum, pp. 198-200]
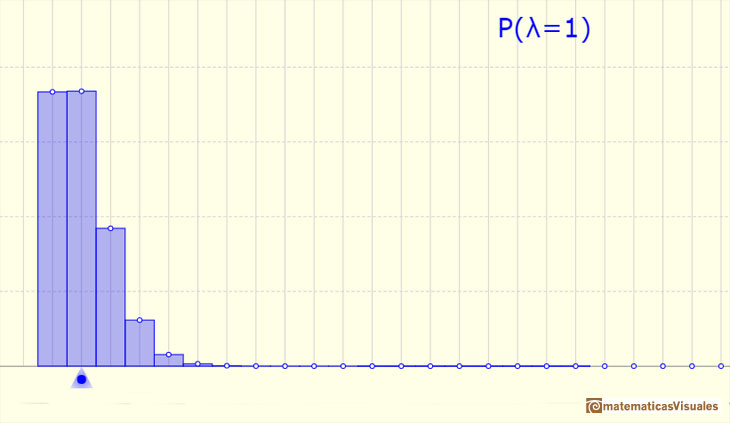
More variability:
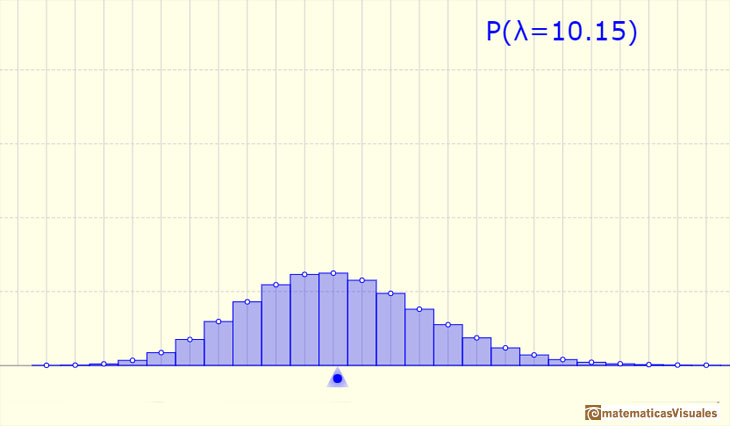
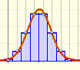
We can approximate a Poisson distribution with the Normal distribution (mean and variance equal to lambda). To use this Normal approximation we make the continuity correction.
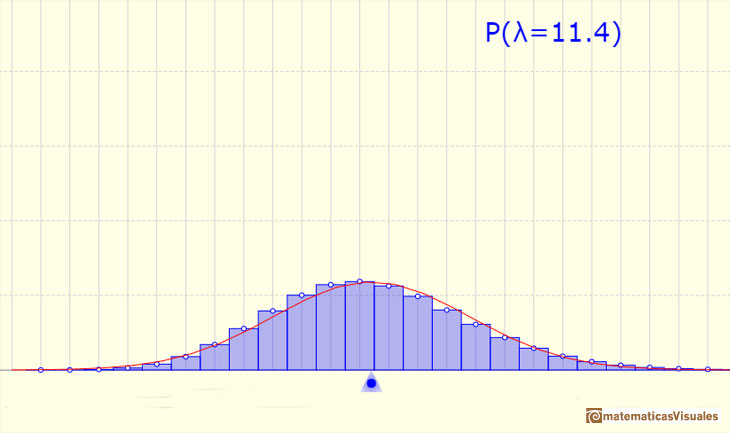
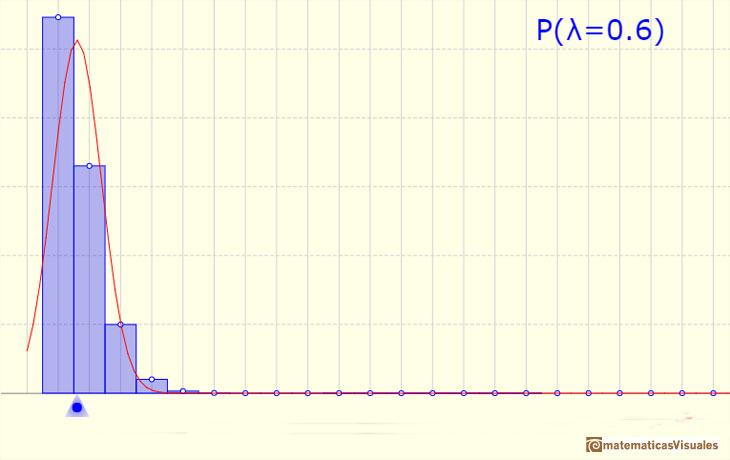
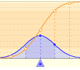
The mean is represented by a triangle and it can be seen as a point of equilibrium. Dragging it we modify the lambda parameter.
We can show a normal curve that has the same mean and variance that the Poisson distribution. This normal curve approximate the Poisson distribution in some cases.
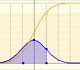
The red dots control vertical and horizontal scales. Pressing and dragging the right button we can move the graphic left and right.
REFERENCES
 NEXT
NEXT
 PREVIOUS
PREVIOUS
MORE LINKS