Matematicas Visuales | Normal Distributions: Probability of Symmetric Intervals

Using the (cumulative) distribution function we can calculate the probability of any interval:

Normal Distributions: (Cumulative) Distribution Function

The (cumulative) distribution function of a random variable X, evaluated at x, is the probability that X will take a value less than or equal to x. In this page we study the Normal Distribution.

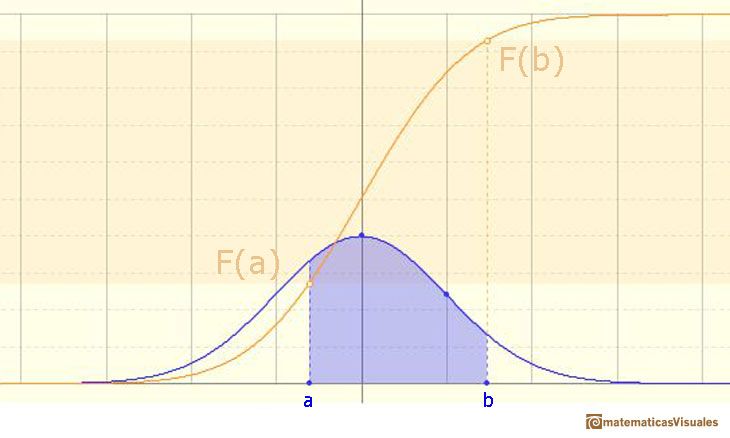
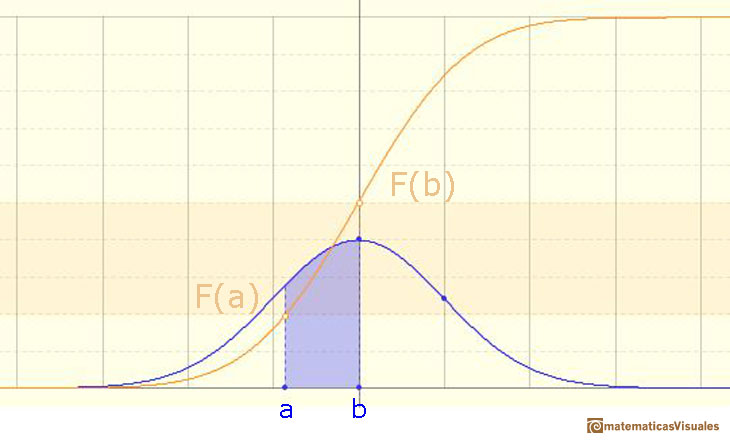
Normal distribution: Cumulative Distribution Function: probability of intervals | matematicasVisuales

In this page we are going to study one simple and interesting case: symmetric intervals around the mean.

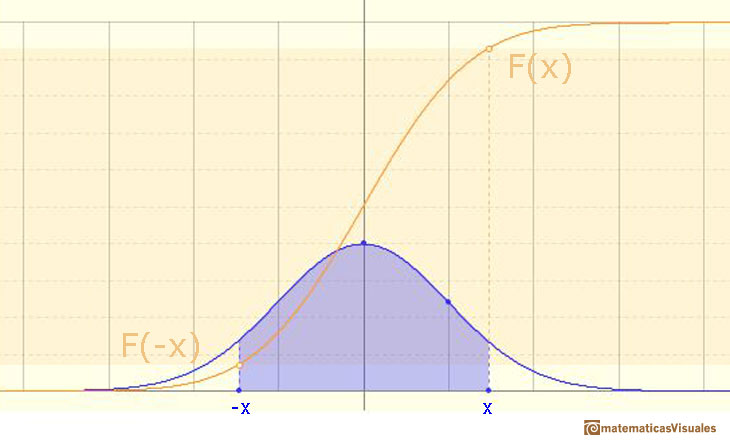
Normal distribution: probability of symmetric intervals | matematicasVisuales

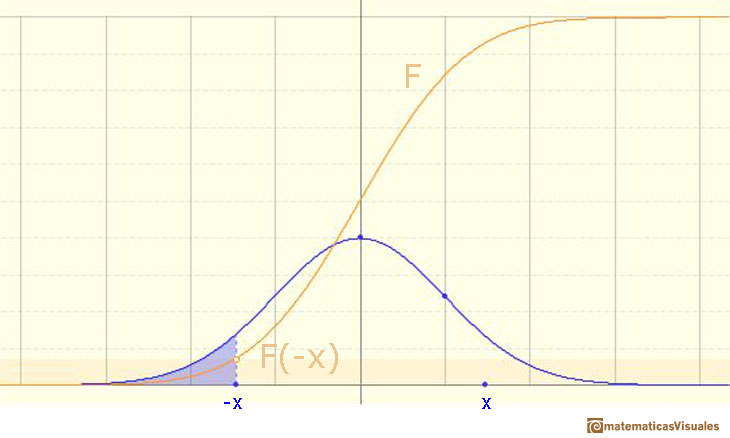
Normal distribution: probability of a left queue | matematicasVisuales

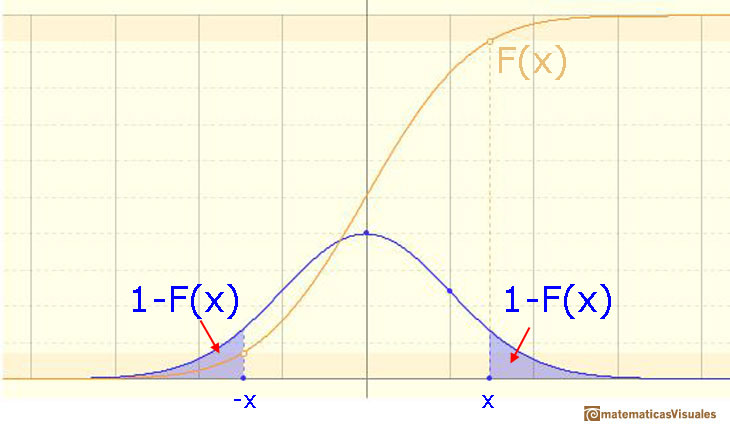
Normal distribution: probability of two queues| matematicasVisuales

Then

We can modifying the parameters of the normal distribution.

The mean is represented by a triangle that can be seen as an equilibrium point. By dragging it we can modify the mean.

Dragging the point on the curve (which is one of the two inflexion points of the curve) we modify the standard deviation.

Moving the blue point on the X-axis we can change the symmetric interval.

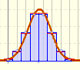
We can see the cumulative distribution function and how it change by modifiyng the mean (simple translation) and the standard deviation (reflecting greater or lesser dispersion of the variable).

The red dots control the vertical and horizontal scales of the graphic.

REFERENCES

George Marsaglia's article Evaluating the Normal Distribution.

Saul Stahl's article The Evolution of the Normal Distribution (Mathematics Magazine, vol. 79, (2006), pp. 96-113. From Mathematical Association of America).

next NEXT

Student's t-distributions

Student's t-distributions were studied by William Gosset(1876-1937) when working with small samples.

Normal Distributions: (Cumulative) Distribution Function

The (cumulative) distribution function of a random variable X, evaluated at x, is the probability that X will take a value less than or equal to x. In this page we study the Normal Distribution.

MORE LINKS

Calculating probabilities in t Student distributions (Spanish)

Binomial distribution

When modeling a situation where there are n independent trials with a constant probability p of success in each test we use a binomial distribution.

Normal approximation to Binomial distribution

In some cases, a Binomial distribution can be approximated by a Normal distribution with the same mean and variance.

Normal distributions

The Normal distribution was studied by Gauss. This is a continuous random variable (the variable can take any real value). The density function is shaped like a bell.

Normal Distributions: One, two and three standard deviations

One important property of normal distributions is that if we consider intervals centered on the mean and a certain extent proportional to the standard deviation, the probability of these intervals is constant regardless of the mean and standard deviation of the normal distribution considered.

Poisson distribution

Poisson distribution is discrete (like the binomial) because the values that can take the random variable are natural numbers, although in the Poisson distribution all the possible cases are theoretically infinite.