After studying Linear Rational Functions we are going to consider rational functions that have a denominator that is a degree 2 polynomial (a parabola).

The simplest case happens when the numerator is a constant and the denominator is a degree 2 polynomial.

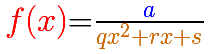
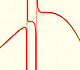
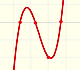
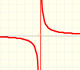
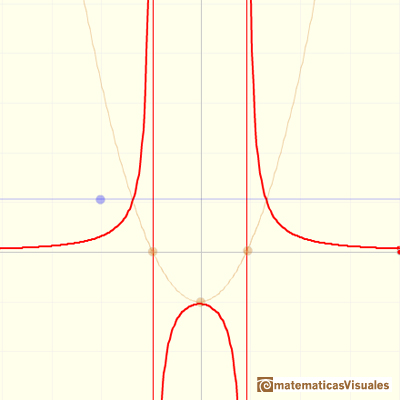
This kind of rational functions may have two vertical asymptotes:

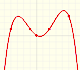
Only one vertical asymptote:

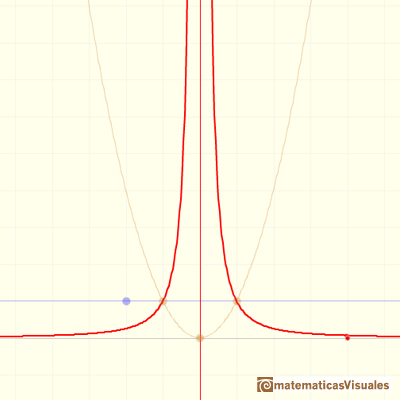
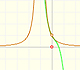
Or no vertical asymptote at all. It depends of the roots of the denominator (and, in some ways depends on the roots of the numerator).

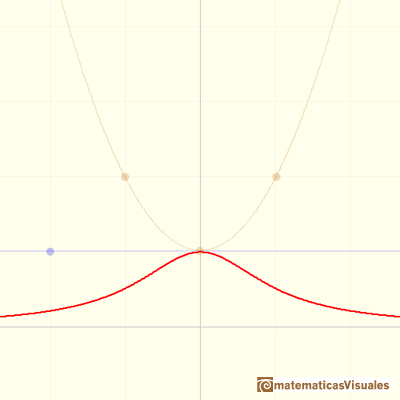
Roots of the denominator are values for which the function is undefined. You can not divide by zero. This values are called singularities of the function. This is interesting to study the function behavior near a singularity. In some cases, depending on the behavior near the singularity, the rational function has a vertical asymptote, as we have already seen in some examples.

In general, if x₀ and x₁ are two roots of the denominator

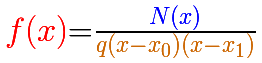
Then, the domain of the rational function is:

If we consider the extreme case when the numerator is equal to 0, the rational function is the horizontal line y=0 but with two holes, one hole or no holes.

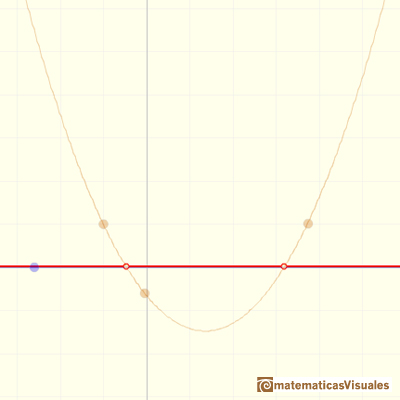
This kind of functions always have one horizontal asymptote (y=0)

Now we are going to consider rational functions that have in the numerator a polynomial of degree 1 (a non-horizontal straight line):

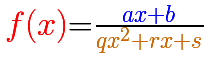
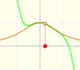
In the next mathlet you can play with this two elements of this kind of rational function: a straight line (the numerator, in blue) and a parabola (the denominator, in orange)

As before, this rational function can have 2, 1 or 0 singularities. It is interesting to study the behavior near the singularities depending on the position of the point where the straight line cuts the x-axis:

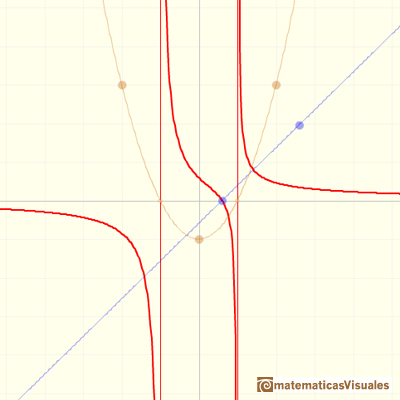
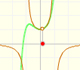
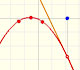
When the function has two singularities and the numerator cut the x-axis in one of these points, then in this singularity we do not have an asymptote but a 'hole'. We call this singularity an avoidable singularity.

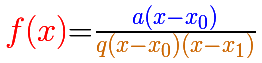
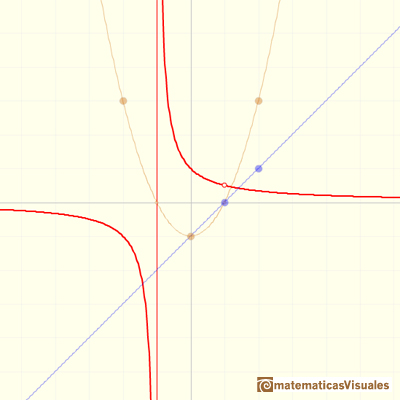
For example, in the previous graph the formula is:

Notice that the numerator and the denominator have (x-1) as a common factor.

Another different case is when the function has a singularity but of degree 2 (the parabola only touches the x-axis, the degree 2 polynomial of de denominator has a double root) and the numerator has the same root, then we have an asymptote.

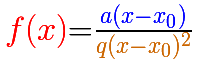
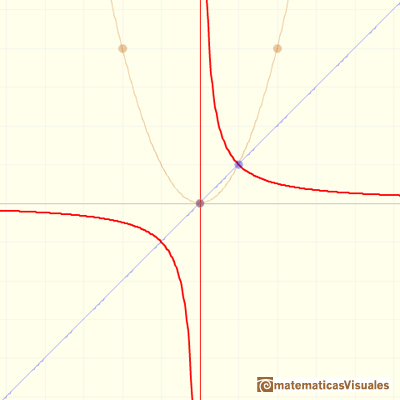
For example, in the previous graph the formula is:

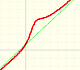
You can see that in some cases the graph of the function cuts the horizontal asymptote y = 0:

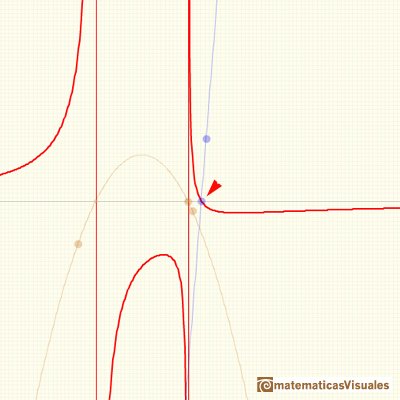
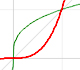
You can add a constant function p to a proper rational function with a denominator of degree 2:

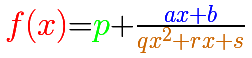
In the next video we can see the three elements of this kind of rational function: a number p (in green a horizontal line), the numerator (a straight line, in blue) and the denominator (a parabola, in orange)

This kind of rational functions has a horizontal asymptote:

When we say that a rational function with a degree 2 polynomial in the denominator can have two, one or none singularities we are thinking about real singularities. When we consider these functions as Complex Functions then these functions always have two (real or) complex singularities. (This is a consequence of the Fundamental Theorem of Algebra, proved by Gauss).

MORE LINKS

Rational Functions (4): Asymptotic behavior

You can add a polynomial to a proper rational function. The end behavior of this rational function is very similar to the polynomial.

Polynomial Functions (1): Linear functions

Two points determine a stright line. As a function we call it a linear function. We can see the slope of a line and how we can get the equation of a line through two points. We study also the x-intercept and the y-intercept of a linear equation.

Polynomial Functions (2): Quadratic functions

Polynomials of degree 2 are quadratic functions. Their graphs are parabolas. To find the x-intercepts we have to solve a quadratic equation. The vertex of a parabola is a maximum of minimum of the function.

Powers with natural exponents (and positive rational exponents)

Power with natural exponents are simple and important functions. Their inverse functions are power with rational exponents (a radical or a nth root)

Polynomial Functions (3): Cubic functions

Polynomials of degree 3 are cubic functions. A real cubic function always crosses the x-axis at least once.

Polynomial Functions (4): Lagrange interpolating polynomial

We can consider the polynomial function that passes through a series of points of the plane. This is an interpolation problem that is solved here using the Lagrange interpolating polynomial.

Taylor polynomials (4): Rational function 1

The function has a singularity at -1. Taylor polynomials about the origin approximates the function between -1 and 1.

Taylor polynomials (5): Rational function 2

The function has a singularity at -1. Taylor polynomials about the origin approximates the function between -1 and 1.

Taylor polynomials (6): Rational function with two real singularities

This function has two real singularities at -1 and 1. Taylor polynomials approximate the function in an interval centered at the center of the series. Its radius is the distance to the nearest singularity.

Taylor polynomials (7): Rational function without real singularities

This is a continuos function and has no real singularities. However, the Taylor series approximates the function only in an interval. To understand this behavior we should consider a complex function.

Taylor polynomials: Rational function with two complex singularities

We will see how Taylor polynomials approximate the function inside its circle of convergence.

Complex Polynomial Functions(1): Powers with natural exponent

Complex power functions with natural exponent have a zero (or root) of multiplicity n in the origin.

Complex Polynomial Functions(2): Polynomial of degree 2

A polynomial of degree 2 has two zeros or roots. In this representation you can see Cassini ovals and a lemniscate.

Complex Polynomial Functions(3): Polynomial of degree 3

A complex polinomial of degree 3 has three roots or zeros.

Complex Polynomial Functions(4): Polynomial of degree n

Every complex polynomial of degree n has n zeros or roots.

Polynomial functions and derivative (1): Linear functions

The derivative of a lineal function is a constant function.

Polynomial functions and derivative (2): Quadratic functions

The derivative of a quadratic function is a linear function, it is to say, a straight line.

Polynomial functions and derivative (3): Cubic functions

The derivative of a cubic function is a quadratic function, a parabola.

Definite integral

The integral concept is associate to the concept of area. We began considering the area limited by the graph of a function and the x-axis between two vertical lines.