Following Tristan Needham, we are going to study two rational functions more to have a better understanding of the convergence of the power series, what he has called "The Mistery of Real Power Series".

We know that many real functions F(x) can be expressed (e.g. via Taylor's Theorem) as power series, and that this infinte series will normally only converge to F(x) in some interval of convergence -R < x < R. But how is R (the radius of convergence) determined by F(x)?.

Needham wrote: "It turns out that this question has a beautifully simple answer, but only if we investigate it in the complex plane. If we instead restrict ourselves to the real line -as mathematicians were forced to in the era in which such series were first employed- then the relationship between R and F(x) is utterly mysterious. Historically, it was precisely this mystery that led Cauchy to several of his breakthroughs in complex analysis." (Tristan Needham, Visual Complex Analysis, p. 64)

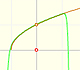
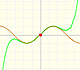
Consider the rational function

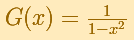
Its series, centered at the origin, has the interval of convergence (-1, 1).

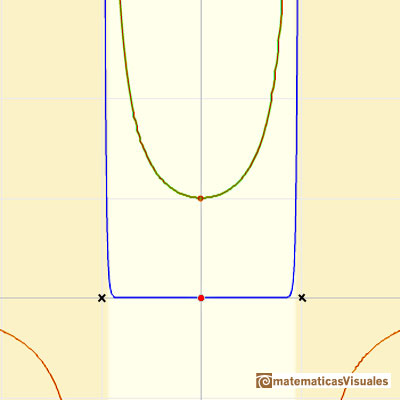
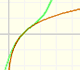
It is easy to understand the interval of convergence of the series because the points x = 1 and x = -1 are singularities of the function itself. They are places where the module of the function becomes infinite.

This behavior is similar to other functions with singularities.

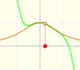
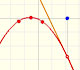
If we change the center of the power series, the radius of the interval of convergence is the distance from the center of the series to the nearest singularity. Singularities act like barriers.

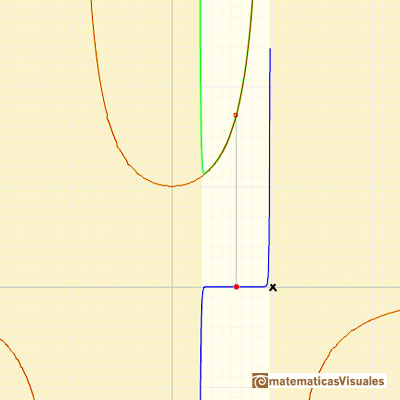
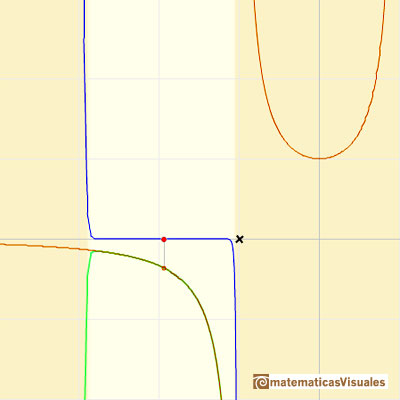
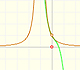
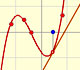
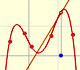
We can compare this behavior with that of another function with a more mysterious behavior: Taylor polynomials (7): Rational function without real singularities.

REFERENCES

MORE LINKS

Taylor polynomials: Rational function with two complex singularities

We will see how Taylor polynomials approximate the function inside its circle of convergence.

Taylor polynomials (1): Exponential function

By increasing the degree, Taylor polynomial approximates the exponential function more and more.

Taylor polynomials (2): Sine function

By increasing the degree, Taylor polynomial approximates the sine function more and more.

Taylor polynomials (3): Square root

The function is not defined for values less than -1. Taylor polynomials about the origin approximates the function between -1 and 1.

Taylor polynomials (4): Rational function 1

The function has a singularity at -1. Taylor polynomials about the origin approximates the function between -1 and 1.

Mercator and Euler: Logarithm Function

Mercator published his famous series for the Logarithm Function in 1668. Euler discovered a practical series to calculate.

Polynomial functions and derivative (1): Linear functions

The derivative of a lineal function is a constant function.

Polynomial functions and derivative (2): Quadratic functions

The derivative of a quadratic function is a linear function, it is to say, a straight line.

Polynomial functions and derivative (3): Cubic functions

The derivative of a cubic function is a quadratic function, a parabola.

Polynomial functions and derivative (4): Lagrange polynomials (General polynomial functions)

Lagrange polynomials are polynomials that pases through n given points. We use Lagrange polynomials to explore a general polynomial function and its derivative.