We are going to study the complex function

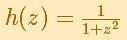
This complex function helps us to understand the behavior of the Taylor series of a real function that has no real singularity. This real function coincides with the complex function in the real axis:

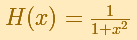
The real function has no singularities but the complex one has two singularities, in z = i and in z = -i.

If we consider complex power series centered at some point, there exists a circle centered at this point such that the series converges everywhere inside the circle and diverges everywhere outside the circle. We are going to see that the radius of convergence is the distance from the center to the nearest singularity.

It is a very important fact that if this series converges at a point, then its value can be approximated by a partail sum (polynomial), and by choosing a sufficiently large degree we can make the approximation as accurate as we wish. (Tristan Needham)

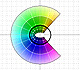
For example, this is a representation of the Taylor's polynomial of degree 6:

The Remainder is the difference between the function and the polynomial. A clear color, almost white, indicates a small module. As we increases the degree of the polynomial the white area approximates the circle of convergence.

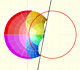
This is a representation of the remainder when we consider the Taylor's polynomial of degree 6. The approximation is very accurate near the center:

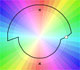
The approximation is better when we consider the polynomial of degree 50:

If we restric our vision to the circle of convergence we can see how these polynomials approximate the function inside the circle of convergence.

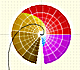
This is a representation of the Taylor's polynomial of degree 50 only inside the circle of convergence:

And this is a representation of the function only inside the same circle. We can see that the image below is very similar to this.

Another example, when the Taylor's polynomial has only degree 15:

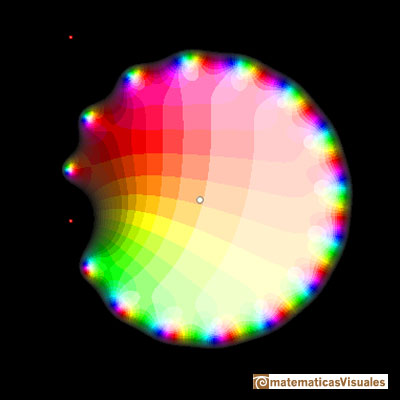
The same polynomial but only inside the circle of convergence:

And the function restricted to the same circle:

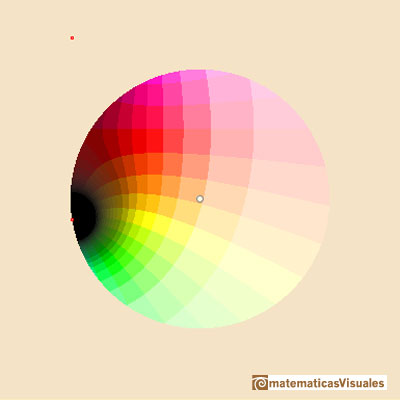
Inside the circle of convergence the function and the approximation are similar but outside they are very different.

MORE LINKS

Complex Polynomial Functions(1): Powers with natural exponent

Complex power functions with natural exponent have a zero (or root) of multiplicity n in the origin.

Complex Polynomial Functions(2): Polynomial of degree 2

A polynomial of degree 2 has two zeros or roots. In this representation you can see Cassini ovals and a lemniscate.

Complex Polynomial Functions(3): Polynomial of degree 3

A complex polinomial of degree 3 has three roots or zeros.

Complex Polynomial Functions(4): Polynomial of degree n

Every complex polynomial of degree n has n zeros or roots.

Complex Polynomial Functions(5): Polynomial of degree n (variant)

Every complex polynomial of degree n has n zeros or roots.

Cero and polo (Spanish)

Podemos modificar las multiplicidades del cero y del polo de estas funciones sencillas.

Cero and polo (variant) (Spanish)

The Complex Exponential Function

The Complex Exponential Function extends the Real Exponential Function to the complex plane.

The Complex Cosine Function

The Complex Cosine Function extends the Real Cosine Function to the complex plane. It is a periodic function that shares several properties with his real ancestor.

The Complex Cosine Function: mapping an horizontal line

The Complex Cosine Function maps horizontal lines to confocal ellipses.

Multifunctions: Powers with fractional exponent

The usual definition of a function is restrictive. We may broaden the definition of a function to allow f(z) to have many differente values for a single value of z. In this case f is called a many-valued function or a multifunction.

Inversion

Inversion is a plane transformation that transform straight lines and circles in straight lines and circles.

Inversion: an anticonformal transformation

Inversion preserves the magnitud of angles but the sense is reversed. Orthogonal circles are mapped into orthogonal circles

Taylor polynomials: Complex Cosine Function

The power series of the Cosine Function converges everywhere in the complex plane.

Taylor polynomials: Rational function with two complex singularities

We will see how Taylor polynomials approximate the function inside its circle of convergence.