We have already seen a multifunction. It is the case of the cubic root that has three values and the point z=0 is called a branch point. Fractional powers are multifunctions.
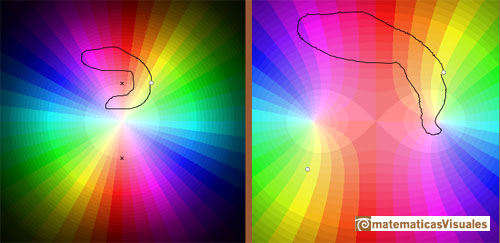
Now we are considering the two-valued multifunction
We can draw a path on the left panel and see how this path is transformed on the right panel.
If z travels along a closed loop like in this picture, not encircling any of the two branch points, its image f(z)
travels along a closed loop and
returns to its original value.
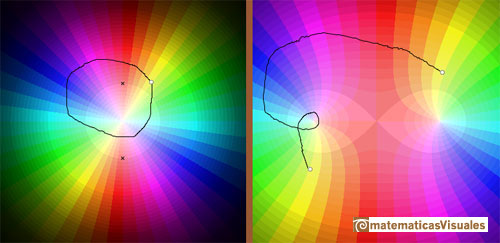
However, if z instead travels along a closed loop which goes round only one of the branch points, then f(z) does not
return to its original value but instead ends up at a different value of the multifunction.
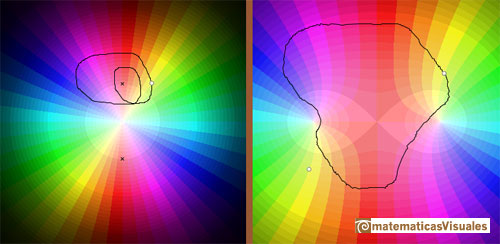
Similarly, if z travels along a closed loop encircling one of the branch points twice, then f(z)
returns to its original value again.
The same happens if the closed loop goes round both branch points.
MORE LINKS

Complex power functions with natural exponent have a zero (or root) of multiplicity n in the origin.

A polynomial of degree 2 has two zeros or roots. In this representation you can see Cassini ovals and a lemniscate.

A complex polinomial of degree 3 has three roots or zeros.

Every complex polynomial of degree n has n zeros or roots.

Every complex polynomial of degree n has n zeros or roots.

Podemos modificar las multiplicidades del cero y del polo de estas funciones sencillas.
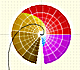
The Complex Exponential Function extends the Real Exponential Function to the complex plane.
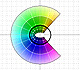
The Complex Cosine Function extends the Real Cosine Function to the complex plane. It is a periodic function that shares several properties with his real ancestor.

The Complex Cosine Function maps horizontal lines to confocal ellipses.
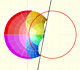
Inversion is a plane transformation that transform straight lines and circles in straight lines and circles.

Inversion preserves the magnitud of angles but the sense is reversed. Orthogonal circles are mapped into orthogonal circles

The complex exponential function is periodic. His power series converges everywhere in the complex plane.

The power series of the Cosine Function converges everywhere in the complex plane.

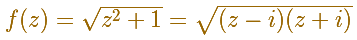

 PREVIOUS
PREVIOUS



















 NEXT
NEXT









