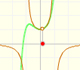
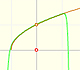
This rational function

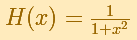
is a continuos function. It has no singularities. Then we could expect that the behavior of its power series is similar to that of other continuous functions such as the exponential function or the sine function. that is to say that the power series would converge in all the real numbers.

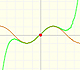
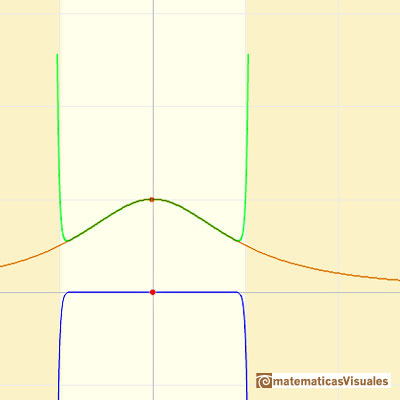
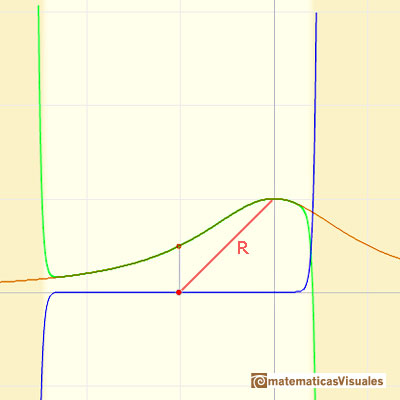
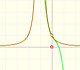
But it is not the case. Although the reason is not clear, the Taylor series is behaving in a manner similar to other non continuous functions, for example, this function with two real singularities. In that case, the radius of convergence is the distance from the center of the power series to the nearest singularity. But in this case we have no real singularity.

The power series converges in an interval centered at the center of the development but not outside it.

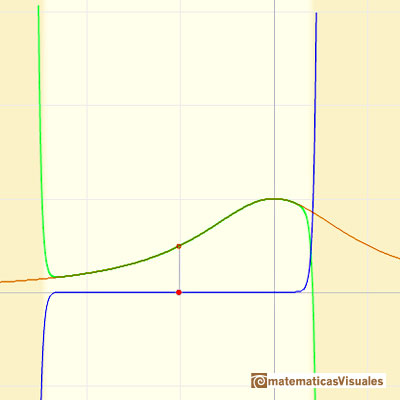
The radius of convergence, R, seems to be the distance from the center of the expansion to either of the fixed points that lie off the line, one unit from 0 in a direction at right angles to the line. If the plane is thought of as the complex plane, these points are +i and -i.

This behavior seems mysterious. What prevents that the series converges everywhere? "The mystery begins to unravel when we turn to the complex function

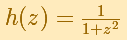
which is identical to H(x) when z is restricted to the real axis of the complex plane." (Tristan Needham)

It si clear that the function has two complex singularities at z = i and at z = -i. The Taylor series converges inside a circle with a radius of convergence that is the distance to the nearest singularity. And this is what we can see in the case of the real function: the radius of the interval of convergence is the distance from the center of the series to the point i in the complex plane.

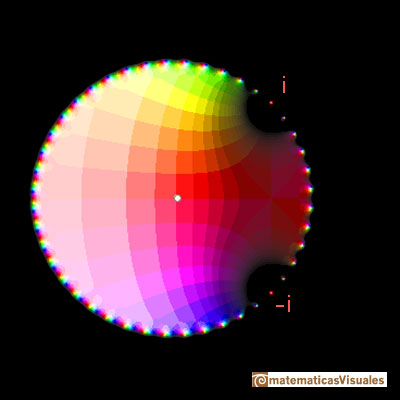
You can see more about this complex function goint to Taylor polynomials: Rational function with two complex singularities.

REFERENCES

MORE LINKS

Mercator and Euler: Logarithm Function

Mercator published his famous series for the Logarithm Function in 1668. Euler discovered a practical series to calculate.

Taylor polynomials (1): Exponential function

By increasing the degree, Taylor polynomial approximates the exponential function more and more.

Taylor polynomials (2): Sine function

By increasing the degree, Taylor polynomial approximates the sine function more and more.

Taylor polynomials (3): Square root

The function is not defined for values less than -1. Taylor polynomials about the origin approximates the function between -1 and 1.

Taylor polynomials (4): Rational function 1

The function has a singularity at -1. Taylor polynomials about the origin approximates the function between -1 and 1.

Taylor polynomials (5): Rational function 2

The function has a singularity at -1. Taylor polynomials about the origin approximates the function between -1 and 1.

Taylor polynomials: Complex Exponential Function

The complex exponential function is periodic. His power series converges everywhere in the complex plane.

Taylor polynomials: Complex Cosine Function

The power series of the Cosine Function converges everywhere in the complex plane.

Polynomial functions and derivative (1): Linear functions

The derivative of a lineal function is a constant function.

Polynomial functions and derivative (2): Quadratic functions

The derivative of a quadratic function is a linear function, it is to say, a straight line.

Polynomial functions and derivative (3): Cubic functions

The derivative of a cubic function is a quadratic function, a parabola.

Polynomial functions and derivative (4): Lagrange polynomials (General polynomial functions)

Lagrange polynomials are polynomials that pases through n given points. We use Lagrange polynomials to explore a general polynomial function and its derivative.