After viewing lineal, quadratic and cubic functions, we can play here with polynomials of higher degrees.
One interesting method of generating polynomial functions is using the so called Lagrange interpolating polynomials.
Our purpose here is to have a better understanding of the behavior of different polynomial functions and their derivatives.
THE CONCEPT OF DERIVATIVE OF A FUNCTION
The derivative of a function at a point can be defined as the instantaneous rate of change or as the slope of the tangent line to the graph of the function at this point. We can say that this slope of the tangent of a function at a point is the slope of the function.
The slope of a function will, in general, depend on x. Then, starting from a function we can get a new function, the derivative function of the original function.
The process of finding the derivative of a function is called differentiation.
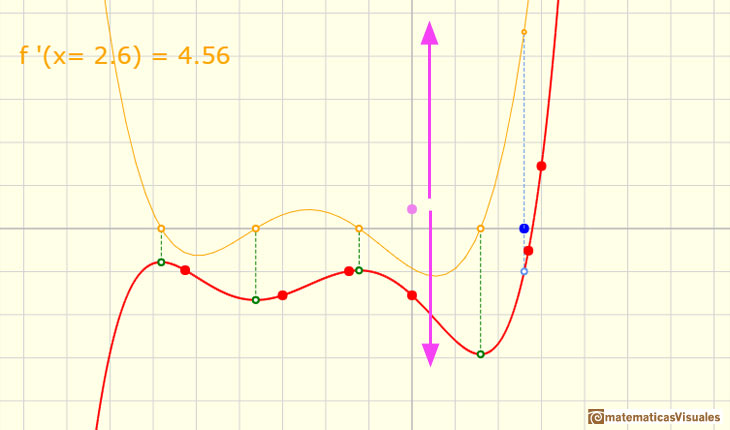
The value of the derivative function for any value x is the slope of the original function at x.
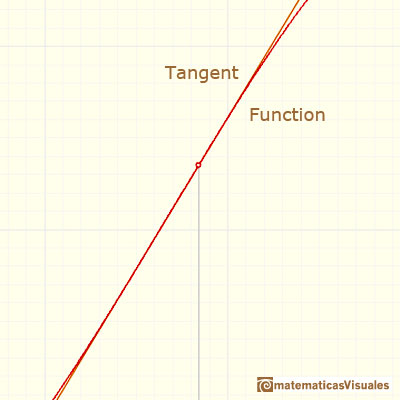
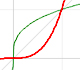
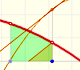
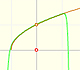
We can review here several concepts that we have already studied. For example, the geometric interpretation of the derivative as the slope of the tangent:
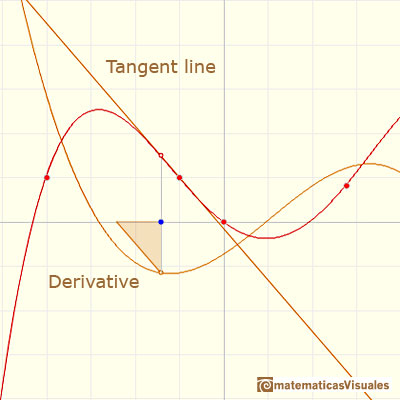
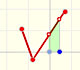
But how can we draw a tangent line?. We can use a magnifying glass!. If we look very near the point in the graph of the function we can see how the function resembles the tangent line. This tangent line is the best linear approximation of the function at that point:
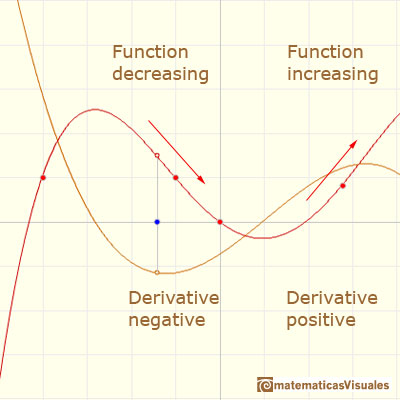
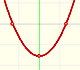
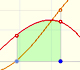
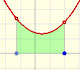
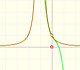
There is a connection between the derivative and the increasing or decreasing of a (polynomial) function. If the derivative is positive in some interval then the function increases in this interval and if the derivative in negative in some interval then the function decreases in this interval:
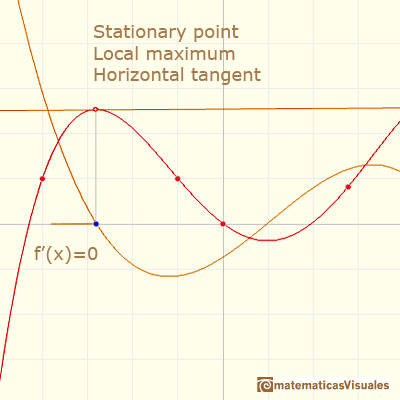
A stationary point is a point where the derivative vanishes (the slope of the tangent is zero, the tangent is an horizontal line). In these points the function stops increasing or decreasing.
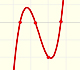
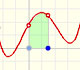
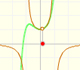
At a stationary point the function can change from increasing to decreasing. Then this stationary point is a local maximum (or relative minimum). The derivative changes from positive to negative.
In other cases, at a stationary point the function can change from decreasing to increasing. Then this stationary point is a local minimum (or relative minimum). The derivative changes from negative to positive.
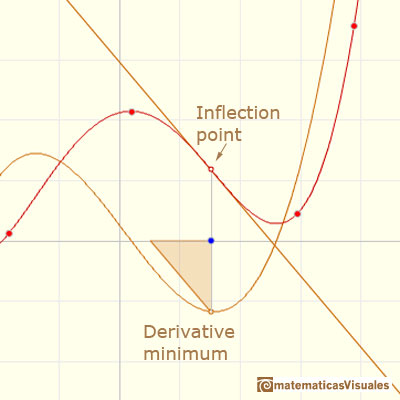
Some times, stationary points are not maxima nor minima. They can be inflection points, points at which the sign of the curvature changes.
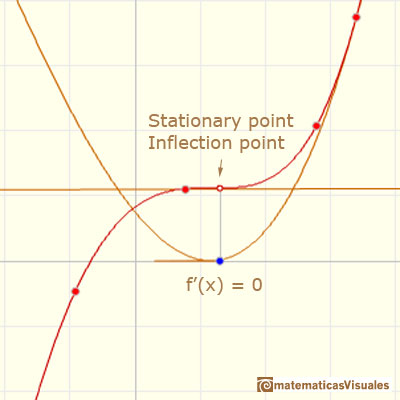
Inflection points are related with local maxima or minima of the derivative function. At these points the tangent crosses the curve.
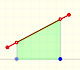
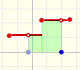
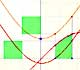
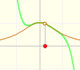
One simple and interesting idea is that when we translate up and down the graph of a function (we add or subtract a number from the original function) the derivative does not change. The reason is very intuitive and we can play with the interactive application to see this property. When you move the violet dot you are translating up and down the graph and the derivative is the same:
It is important to notice that the derivative of a polynomial of degree 1 is a constant function (a polynomial of degree 0). The derivative of a polinomial of degree 2 is a polynomial of degree 1. And the derivative of a polynomial of degree 3 is a polynomial of degree 2.
When we derive such a polynomial function the result is a polynomial that has a degree 1 less than the original function.
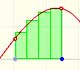
When we study the integral of a polynomial of degree 2 we can see that in this case the new function is a polynomial of degree 3. One degree more than the original function. And the integral of a polynomial function is a polynomial function of degree 1 more than the original function.
These results are related to the Fundamental Theorem of Calculus.
REFERENCES
 NEXT
NEXT
MORE LINKS


















 PREVIOUS
PREVIOUS