"The Logarithmotechnia of Nicolas Mercator (1620-1687)was published in 1668. The first two parts of this book
were devoted entirely to the calculation of a table of common logarithms.(...)
It is the very different third part of the Logarithmotechnia that is now of principal interest. Here Mercator
finds his famous series (apparently used previously by Newton)
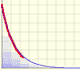
for the area under the hyperbola
over the interval from 0 to x."(Edwards, pag. 162)
It was known in the 1660s, as a consequence of the work of Gregory St. Vincent and de Sarasa, that there is a
relation between the area under the hyperbola and the logarithm.
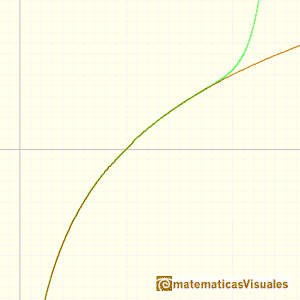
Mercator's series for the Logarithm aproximates the function only between 0 and 2. More than that, its rate of convergence
is very slow and it is not practical to use this serie to calculate logarithms.
Euler replaced x with -x in Mercator's series and then subtract logarithms to obtain
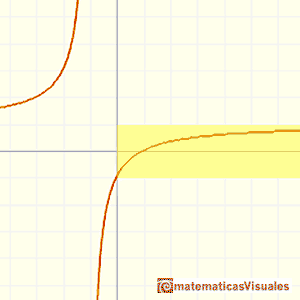
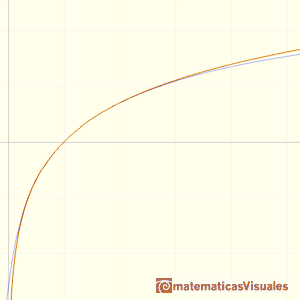
Euler used a rational function
His series converges everywhere.
We can see in the mathlet how fast this series converges.
MORE LINKS
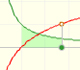
We can study several properties of exponential functions, their derivatives and an introduction to the number e.
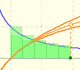
Using the integral of the equilateral hyperbola we can define a new function that is the natural logarithm function.
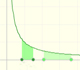
The natural logaritm can be defined using the integral of the rectangular hiperbola. In this page we are going to see an important property of this integral. Using this property you can justify that the logarithm of a product is the sum of the logarithms.
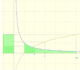
The main property of a logarithm function is that the logarithm of a product is the sum of the logarithms of the individual factors.

Constant e is the number whose natural logarithm is 1. It can be defined as a limit of a sequence related with the compound interest. Both definitions for e are equivalent.
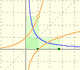
After the definition of the natural logarithm function as an integral you can define the exponential function as the inverse function of the logarithm.

Different hyperbolas allow us to define different logarithms functions and their inversas, exponentials functions.

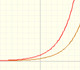
By increasing the degree, Taylor polynomial approximates the exponential function more and more.
The Complex Exponential Function extends the Real Exponential Function to the complex plane.

The complex exponential function is periodic. His power series converges everywhere in the complex plane.

Studying the volume of a barrel, Kepler solved a problem about maxima in 1615.

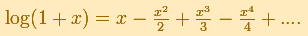
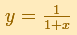
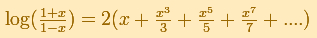
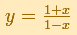
 PREVIOUS
PREVIOUS





















 NEXT
NEXT