In this page we are going to study exponential functions.
You can move the red dots to see the graph of different exponential functions.
Exponential functions are related to geometric progressions:
Geometric sequences graphic representations. Sum of terms of a geometric sequence and geometric series.
Exponential functions can be seen as extensions of geometric succesions to the Real Numbers. But it is not so easy to make this extension.
You can think that it is easy to understand the meaning of a function like 2x
(or 3x or 10x) because we can calculate thinks like
But, the meaning of
There is no simple way to defining 2x for irrational x.
In general, this kind of functions are called Exponential Functions
b is called the base of the exponential function.
We expect that this function satisfy the fundamental equation
And
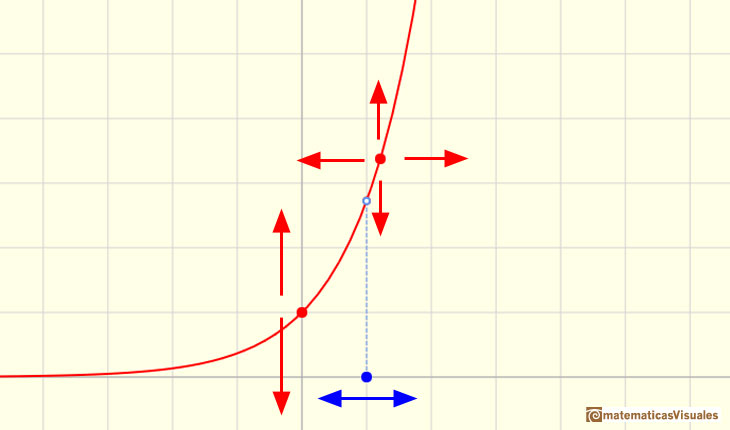
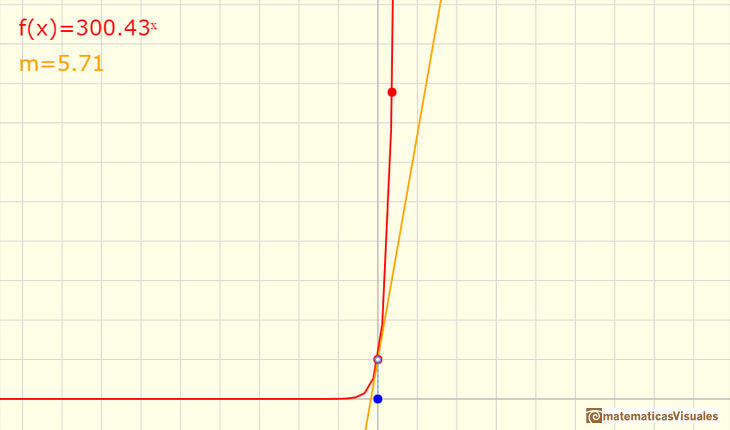
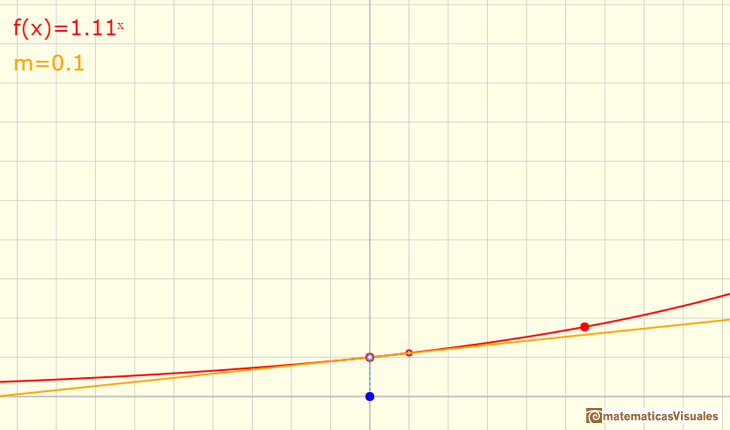
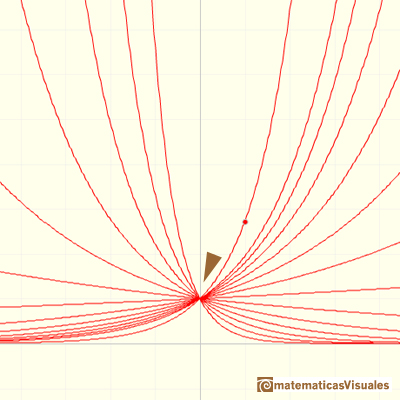
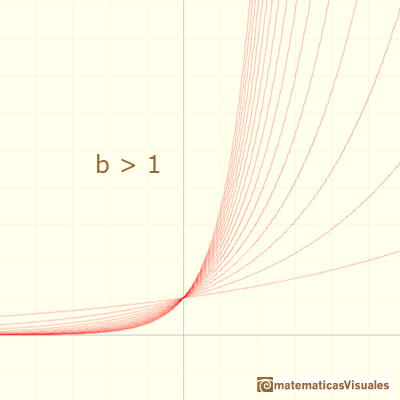
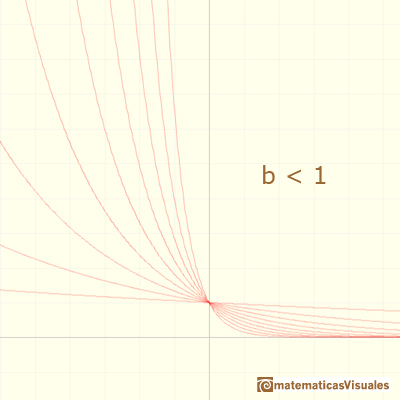
Some of these functions are increasing (when b < 1)
And some are decreasing (when b > 1)
When an exponential function is increasing, 'at the end' it increases very rapidly even if the base is only a little bigger than 1.
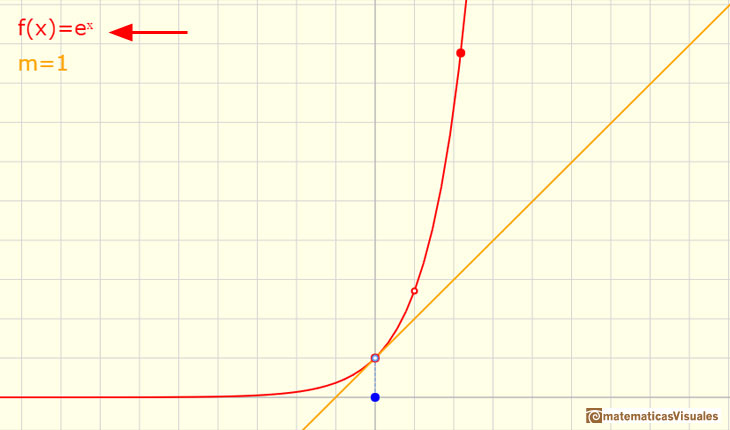
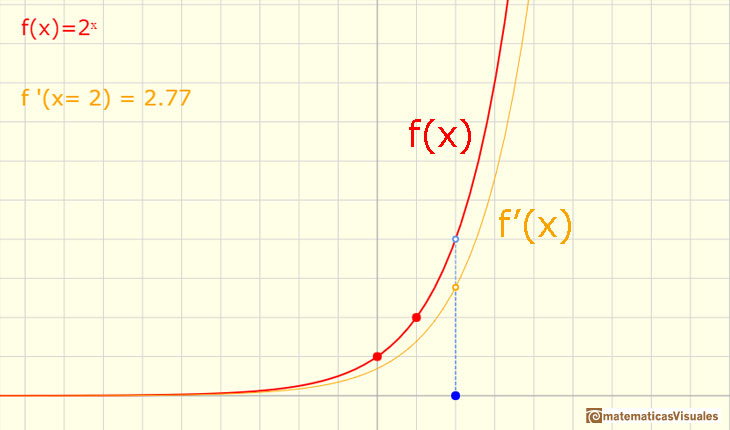
We can see that all exponential functions have a very similar shape. But there is a exponential function very special. Its base is a number but
it seems odd that we call number e (Euler was the first to use this notation for this number).
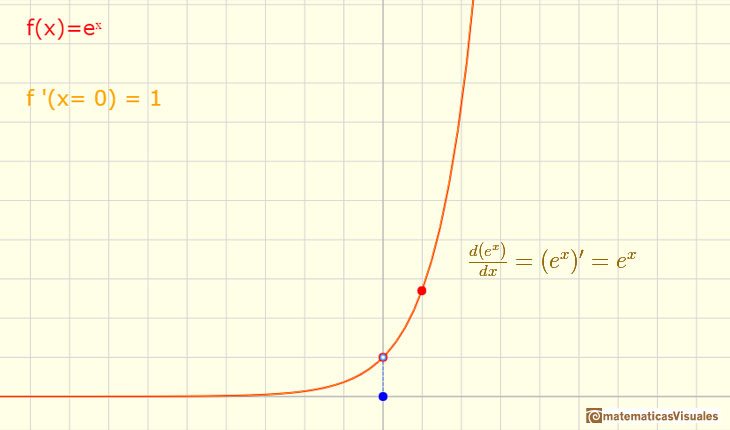
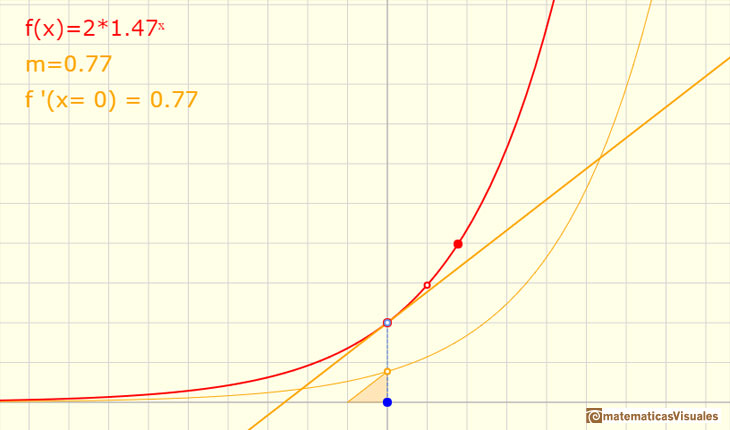
Tangents at 0. Existence of number e
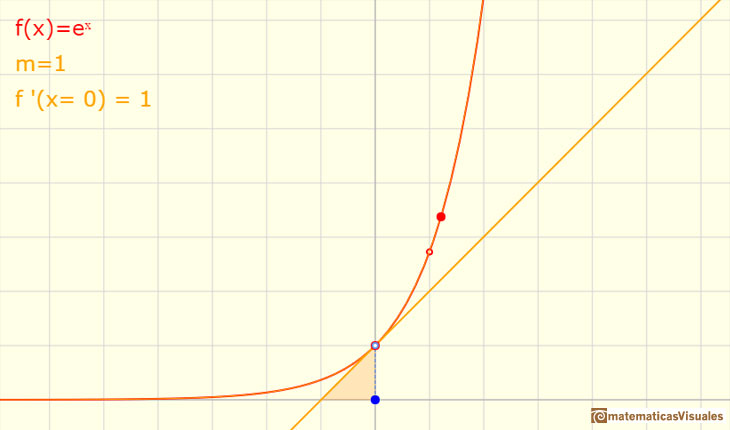
If we look at the tangent at x=0 of such functions there is a base for which the slope of the tangent of the function at x=0 is 1. We are going to call
such number as e
"The existence of a number e having the above property can be motivated as follows. Let a, b be numbers > 1 and suppose that
a < b. Then for all numbers x, we have
If b is very large, then the curve y=bx will have a very steep slope at x=0.
It is plausible that as a increases from numbers close to 1 (and > 1) to very large numbers, the slope of ax at x=0 increases
continuously from values close to 0 to large values, and therefore for some value of a, which we call e, this slope
is precisely equal to 1. Thus in this naive approach, e is the number such that the slope of ex at x=0 is equal to 1. " (Serge Lang)
We shall find out eventually how to compute e. Its value is
Using limits, the slope of the tangent at x= 0 is (if this limit exits)
Notice that, if this limit exists, only depends on b.
Then we are saying that there is a number e such as
Thinking about the derivative of an exponential function, if that limit exits and using the property of the exponentials, we can
write
This is to say, the derivative of an exponential function is a multiple of the function (we do not know yet the value of this factor)
And the number e has a very nice property
INVESTIGATE
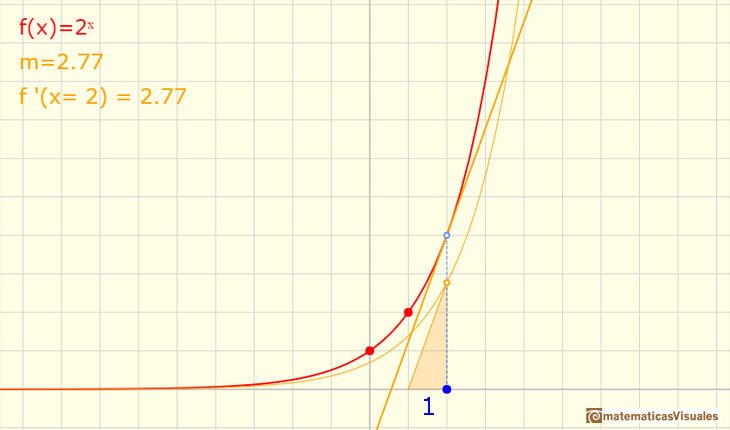
Moving the red point that it is not over the vertical axis you can see different exponential functions. You can see the relation between the
derivative of a function in a point and the tangent line. You can see a right triangle and that the hypotenuse is parallel to the tangent.
What happens when the base is e?.
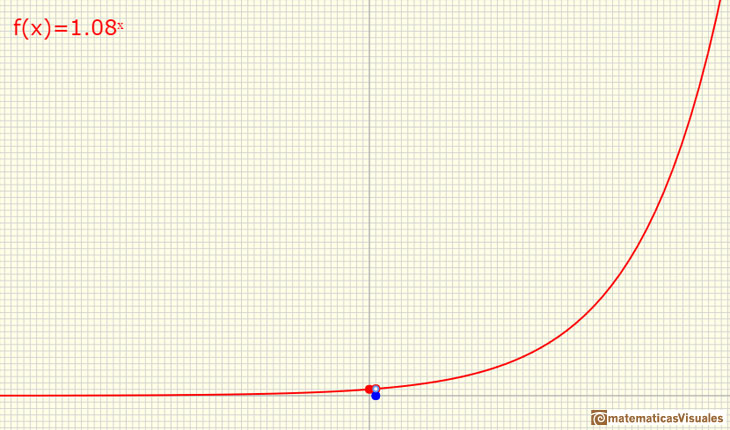
If you move the two red points you can see the graph the more general exponential functions:
An exponential function is
fixed when we know two points.
In this page we played with exponential functions but we have problems with the definition of such functions. Remember that we do not know the
meaning of
The idea is to introduce logarithms first and then use logarithms to define exponential functions.
REFERENCES
A. I. Markushevich, Areas and Logarithms, D.C. Heath and Company, 1963.
Serge Lang, A First Course in Calculus, Third Edition, Addison-Wesley Publishing Company.
Tom M. Apostol, Calculus, Second Edition, John Willey and Sons, Inc.
Michael Spivak, Calculus, Third Edition, Publish-or-Perish, Inc.
Otto Toeplitz, The Calculus, a genetic approach, The University of Chicago Press, 1963.
Kenneth A. Ross, Elementary Analysis: The Theory of Calculus, Springer-Verlag New York Inc., 1980.
 NEXT
NEXT
Using the integral of the equilateral hyperbola we can define a new function that is the natural logarithm function.
 PREVIOUS
PREVIOUS
The integral of power functions was know by Cavalieri from n=1 to n=9. Fermat was able to solve this problem using geometric progressions.
MORE LINKS
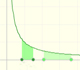
The natural logaritm can be defined using the integral of the rectangular hiperbola. In this page we are going to see an important property of this integral. Using this property you can justify that the logarithm of a product is the sum of the logarithms.
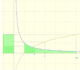
The main property of a logarithm function is that the logarithm of a product is the sum of the logarithms of the individual factors.
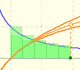
The logarithm of the number e is equal to 1. Using this definition of the number e we can approximate its value.

Constant e is the number whose natural logarithm is 1. It can be defined as a limit of a sequence related with the compound interest. Both definitions for e are equivalent.
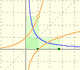
After the definition of the natural logarithm function as an integral you can define the exponential function as the inverse function of the logarithm.

Different hyperbolas allow us to define different logarithms functions and their inversas, exponentials functions.
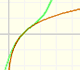
Mercator published his famous series for the Logarithm Function in 1668. Euler discovered a practical series to calculate.

By increasing the degree, Taylor polynomial approximates the exponential function more and more.
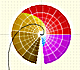
The Complex Exponential Function extends the Real Exponential Function to the complex plane.

The complex exponential function is periodic. His power series converges everywhere in the complex plane.
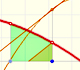
The Fundamental Theorem of Calculus tell us that every continuous function has an antiderivative and shows how to construct one using the integral.
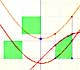
The Second Fundamental Theorem of Calculus is a powerful tool for evaluating definite integral (if we know an antiderivative of the function).
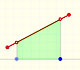
As an introduction to Piecewise Linear Functions we study linear functions restricted to an open interval: their graphs are like segments.
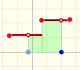
A piecewise function is a function that is defined by several subfunctions. If each piece is a constant function then the piecewise function is called Piecewise constant function or Step function.
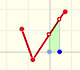
A continuous piecewise linear function is defined by several segments or rays connected, without jumps between them.

The integral of power functions was know by Cavalieri from n=1 to n=9. Fermat was able to solve this problem using geometric progressions.
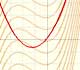
If the derivative of F(x) is f(x), then we say that an indefinite integral of f(x) with respect to x is F(x). We also say that F is an antiderivative or a primitive function of f.
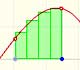
The integral concept is associate to the concept of area. We began considering the area limited by the graph of a function and the x-axis between two vertical lines.

Monotonic functions in a closed interval are integrable. In these cases we can bound the error we make when approximating the integral using rectangles.
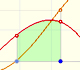
If we consider the lower limit of integration a as fixed and if we can calculate the integral for different values of the upper limit of integration b then we can define a new function: an indefinite integral of f.
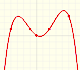
We can consider the polynomial function that passes through a series of points of the plane. This is an interpolation problem that is solved here using the Lagrange interpolating polynomial.



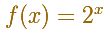
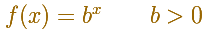



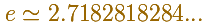
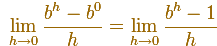
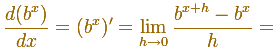
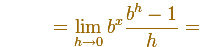
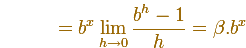
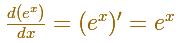
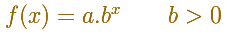
 NEXT
NEXT
 PREVIOUS
PREVIOUS