In his book 'In pursuit of the Unknown', Ian Stewart summarized in a few lines why this equations is so important:
What does it tell us?
How to multiply numbers by adding related numbers instead.
Why is that important?
Addition is much simpler than multiplication.
What did it lead to?
Efficient methods for calculating astronomical phenomena such as eclipses
and planetary orbits. Quick ways to perform scientific calculations. The engineers'
faithful companion, the slide rule. Radioactive decay and the psychophysics of
human perception.
(Ian Stewart, p. 22)
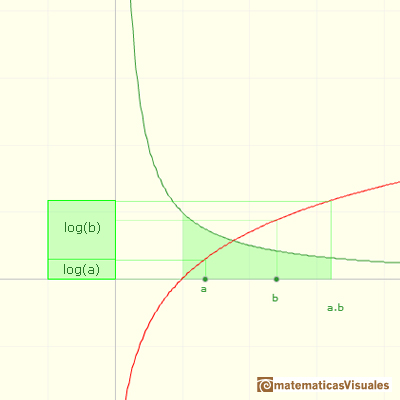
The need for a way to facilitate long operations such as products, divisions and
roots is the origin of the invention of logarithms by Napier.
C.H.Edwards Jr. wrote: "The late sixteenth century was an age of numerical computation, as developments in astronomy and
navegation called for increasingly accurate and lengthy trigonometric computations. (...) The urgent need, for some device to
shorten the labor of tedious multiplications and divisions with many decimal places, was met through the invention of
logarithms by Napier and others around the turn of the seventheenth century.
" (pag. 142).
Napier's logarithmic tables first appeared in 1614. Henry Briggs published in 1624 the first
table of decimal (base 10) logarithms.
REFERENCES
A. I. Markushevich, Areas and Logarithms, D.C. Heath and Company, 1963.
Serge Lang, A First Course in Calculus, Third Edition, Addison-Wesley Publishing Company.
Tom M. Apostol, Calculus, Second Edition, John Willey and Sons, Inc.
Michael Spivak, Calculus, Third Edition, Publish-or-Perish, Inc.
Otto Toeplitz, The Calculus, a genetic approach, The University of Chicago Press, 1963.
Kenneth A. Ross, Elementary Analysis: The Theory of Calculus, Springer-Verlag New York Inc., 1980.
C.H. Edwards, Jr., The Historical Development of the Calculus, Springer-Verlag New York Inc., 1979.
Ian Stewart, In pursuit of the Unknown, 17 Equations that changed the World, Basic Books, 2012.
MORE LINKS
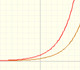
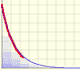
We can study several properties of exponential functions, their derivatives and an introduction to the number e.
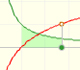
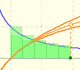
Using the integral of the equilateral hyperbola we can define a new function that is the natural logarithm function.

Constant e is the number whose natural logarithm is 1. It can be defined as a limit of a sequence related with the compound interest. Both definitions for e are equivalent.
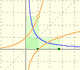
After the definition of the natural logarithm function as an integral you can define the exponential function as the inverse function of the logarithm.

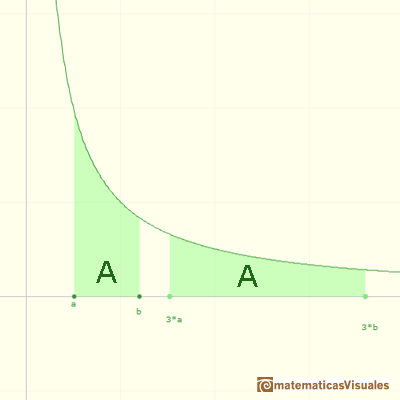
Different hyperbolas allow us to define different logarithms functions and their inversas, exponentials functions.
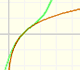
Mercator published his famous series for the Logarithm Function in 1668. Euler discovered a practical series to calculate.

By increasing the degree, Taylor polynomial approximates the exponential function more and more.
The Complex Exponential Function extends the Real Exponential Function to the complex plane.

The complex exponential function is periodic. His power series converges everywhere in the complex plane.
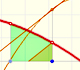
The Fundamental Theorem of Calculus tell us that every continuous function has an antiderivative and shows how to construct one using the integral.
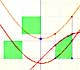
The Second Fundamental Theorem of Calculus is a powerful tool for evaluating definite integral (if we know an antiderivative of the function).
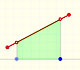
As an introduction to Piecewise Linear Functions we study linear functions restricted to an open interval: their graphs are like segments.
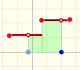
A piecewise function is a function that is defined by several subfunctions. If each piece is a constant function then the piecewise function is called Piecewise constant function or Step function.
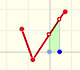
A continuous piecewise linear function is defined by several segments or rays connected, without jumps between them.
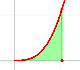
The integral of power functions was know by Cavalieri from n=1 to n=9. Fermat was able to solve this problem using geometric progressions.
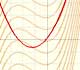
If the derivative of F(x) is f(x), then we say that an indefinite integral of f(x) with respect to x is F(x). We also say that F is an antiderivative or a primitive function of f.
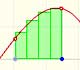
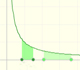
The integral concept is associate to the concept of area. We began considering the area limited by the graph of a function and the x-axis between two vertical lines.

Monotonic functions in a closed interval are integrable. In these cases we can bound the error we make when approximating the integral using rectangles.
If we consider the lower limit of integration a as fixed and if we can calculate the integral for different values of the upper limit of integration b then we can define a new function: an indefinite integral of f.
We can consider the polynomial function that passes through a series of points of the plane. This is an interpolation problem that is solved here using the Lagrange interpolating polynomial.

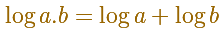
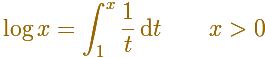
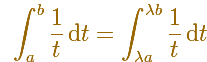
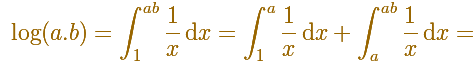
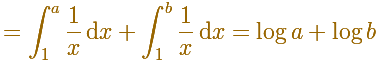
 NEXT
NEXT
 PREVIOUS
PREVIOUS