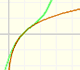
Radioactive Desintegration
Podemos modelar la desintegración radioactiva usando una función exponencial.
El tiempo necesario para que el número de átomos radioactivos quede reducida a la mitad se llama periodo de semidesintegración.
Modificando los puntos cambiamos el número de átomos inicial y el periodo de semidesintegración.
Con los botones generamos el material radioactivo y controlamos el proceso de desintegración
Si el número de átomos es muy grande, la razón entre el número de átomos desintegrados por unidad de tiempo y el número total de átomos es una magnitud constante que depende del tipo de átomo.
Podemos considerar que el hecho de que un átomo se desintegre es independiente de lo que les ocurra al resto. Tomando intervalos de tiempo pequeños, cada átomo se desintegra o no con una determinada probabilidad.
El número de átomos radioactivos que quedan se ajusta aproximadamente a una función exponencial.
REFERENCES
Zeldóvich y Yaglom - Matemáticas superiores. Ed. Mir. (p. 271)
 NEXT
NEXT
 PREVIOUS
PREVIOUS
MORE LINKS
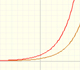
We can study several properties of exponential functions, their derivatives and an introduction to the number e.
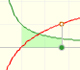
Using the integral of the equilateral hyperbola we can define a new function that is the natural logarithm function.
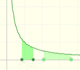
The natural logaritm can be defined using the integral of the rectangular hiperbola. In this page we are going to see an important property of this integral. Using this property you can justify that the logarithm of a product is the sum of the logarithms.
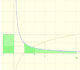
The main property of a logarithm function is that the logarithm of a product is the sum of the logarithms of the individual factors.
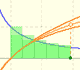
The logarithm of the number e is equal to 1. Using this definition of the number e we can approximate its value.

Constant e is the number whose natural logarithm is 1. It can be defined as a limit of a sequence related with the compound interest. Both definitions for e are equivalent.
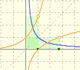
After the definition of the natural logarithm function as an integral you can define the exponential function as the inverse function of the logarithm.

The complex exponential function is periodic. His power series converges everywhere in the complex plane.

The Fundamental Theorem of Calculus tell us that every continuous function has an antiderivative and shows how to construct one using the integral.

The Second Fundamental Theorem of Calculus is a powerful tool for evaluating definite integral (if we know an antiderivative of the function).
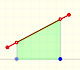
As an introduction to Piecewise Linear Functions we study linear functions restricted to an open interval: their graphs are like segments.
A piecewise function is a function that is defined by several subfunctions. If each piece is a constant function then the piecewise function is called Piecewise constant function or Step function.
A continuous piecewise linear function is defined by several segments or rays connected, without jumps between them.
The integral of power functions was know by Cavalieri from n=1 to n=9. Fermat was able to solve this problem using geometric progressions.
If the derivative of F(x) is f(x), then we say that an indefinite integral of f(x) with respect to x is F(x). We also say that F is an antiderivative or a primitive function of f.

The integral concept is associate to the concept of area. We began considering the area limited by the graph of a function and the x-axis between two vertical lines.

Monotonic functions in a closed interval are integrable. In these cases we can bound the error we make when approximating the integral using rectangles.

If we consider the lower limit of integration a as fixed and if we can calculate the integral for different values of the upper limit of integration b then we can define a new function: an indefinite integral of f.