One important problem related with the origin of Calculus is finding "maxima and minima" of a function. For example, Euclid proved that among all rectangles of equal perimeter the square has the largest area. Fermat (born in 1601) has a different approach and was interested in the tangent of a curve and the relation of this tangent and the maximum (or minimun) of a function. Before Fermat, Kepler (1571-1630) was aware of this relation, though not in the sense of functions and derivatives. He wrote "Nova Stereometria doliorum vinariorum" (1615) a book about the volume of wine barrels and other bodies.

In this page I only try to illustrate Otto Toeplitz's explanation of this episode of the History of Calculus ("The Calculus: A genetic Approach" by Otto Toeplitz):

"Aside from his astronomical works, an instance of this is to be found in his so-called 'Doliometry', the 'barrel calculation'. When he, the imperial court astrologer at Linz, married the second time, he bought for the wedding wine from a barrel. To compute the bill, the wine merchant measured the barrel by inserting a foot rule into the taphole S until it reached the lid at D;

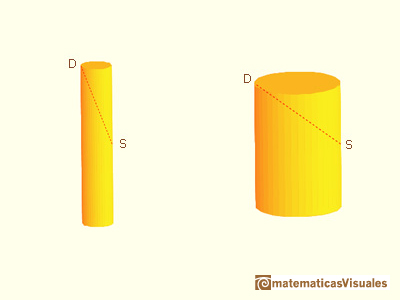
then he read off the length SD = d and set the price accordingly. This method outraged Kepler, who saw that a narrow, high barrel might have the same SD as a wide one and would indicate the same wine price, thought its volume would be ever so much smaller.

Giving further thought to this method of using d to determine the volume, Kepler approximated the barrel somewhat roughly by a cylinder, with v the radius of the base and h the height. Then

or

Hence, the general formula for the volume of a cylinder:

In our case, replacing r for its value:

Notice that the volume is a cubic function of the height:

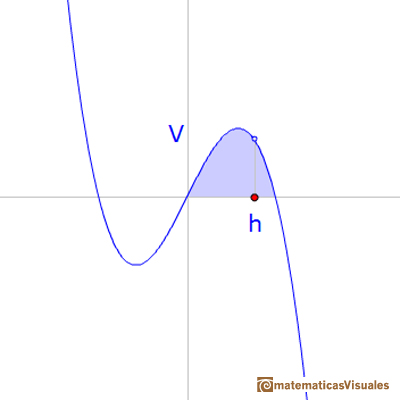
Then he asked: If d is fixed, what value of h gives the largest volume V? V is a polynomial in h; hence the derivative (though of course, Kepler did not use derivatives)

For V to be a maximum, V' must equal zero; hence

That defined a barrel of definite proportions. Kepler noticed that in his Rhenish homeland barrels were narrowed and higher than in Austria, where their shape was peculiarly close to that having a maximum volumen for a fixed d -so close, indeed, that Kepler could not believe this to be a accidental. So he imagined that centuries ago somebody had calculated barrel shapes, as he himself was doing, and had taught the Austrians tho construct their barrels in this particular fashion- a very practical one, indeed. Kepler showed that if a barrel did not satisfy the exact mathematical specification

but deviated somewhat from it, this would have but little effect on the volume, because near its maximum a function changes only slowly.

Thus, while the Austrian method of price determination, if applied to Rhenish barrels, would be a clear fraud, it was quite legitimate for Austrian barrels. The Austrian shape had the advantage of permitting such a quick and simple method. So Kepler relaxed in this instance. Working out finer approximations of various barrel shapes, he consulted Archimedes and discovered that his own method of indivisibles had enabled him to obtain results in a far simpler and more general way than Archimedes, who had been struggling with cumbersome and difficult proofs. What he did not suspect was that Archimedes, too, had found his results by the same method of indivisibles (for the Method was lost until 1906!). Kepler devoted to these problems a whole book containing computations of many volumes." [Otto Toeplitz]

You can see the whole book "Nova Stereometria doliorum vinariorum" in The Posner Library.

You can see a page from Nova Stereometria doliorum vinaniorum, german version, from MathDL.

In the article Kepler: The Volume of a Wine Barrel published by MathDl (Loci, June 2010) I presented a more complete version of this page around the anecdote that lead to Kepler to study volumes of barrels and other bodies and to write his book (published in 1615) "Nova Stereometria doliorum vinariorum" (New solid geometry of wine barrels) where he used some infinitesimal techniques previous to the discovering of differential and integral calculus by Newton and Leibnitz. (In this article some mathlets don't work perfectly well but you can see a full version here).

MORE LINKS

Kepler: The Area of a Circle

Kepler used an intuitive infinitesimal approach to calculate the area of a circle.

Cavalieri: The volume of a sphere

Using Cavalieri's Principle we can calculate the volume of a sphere.

Archimedes' Method to calculate the area of a parabolic segment

Archimedes show us in 'The Method' how to use the lever law to discover the area of a parabolic segment.

Rhombic Dodecahedron (1): honeycombs

Humankind has always been fascinated by how bees build their honeycombs. Kepler related honeycombs with a polyhedron called Rhombic Dodecahedron.

Rhombic Dodecahedron (2): honeycomb minima property

We want to close a hexagonal prism as bees do, using three rhombi. Then, which is the shape of these three rhombi that closes the prism with the minimum surface area?.

Construcción de poliedros. Cuboctaedro y dodecaedro rómbico: Taller de Talento Matemático de Zaragoza 2014 (Spanish)

Material for a session about polyhedra (Zaragoza, 9th May 2014). Simple techniques to build polyhedra like the tetrahedron, octahedron, the cuboctahedron and the rhombic dodecahedron. We can build a box that is a rhombic dodecahedron.