
El pasado 11 de abril de 2020 murió el prestigioso matemático John H. Conway por complicaciones con COVID-19.
Era profesor emérito de la Universidad de Princeton. Hizo importantes contirbuciones a las Matemáticas (por ejemplo, en teoría de grupos) y también se interesó por las Matemáticas recreativas.
Entre otras contribuciones inventó el Juego de la Vida que es el que vamos a comentar ahora.
Me sirvió como disculpa para mostrar una serie de fotografías de Naturaleza en una aplicación desarrollada en Flash con la que he generado esta animación. Al principio y al final de la animación las imágenes se mueven siguiendo un patrón que corresponde con el de una colonia del Juego de la Vida que se llama deslizador.
La siguiente imagen muestra la colonia que es el pequeño deslizador que ha inspirado la animación. Está formado por 5 individuos que simulan un desplazamiento diagonal.

Más adelante se verán más detalles de lo que son los deslizadores en el Juego de la Vida y algún ejemplo más.
Se puede interactuar con la animación a partir del siguiente enlace (requiere Flash Player):

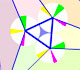
También ideó está demostración del teorema de Morley: un teorema fácil de enunciar pero dificil de probar.
El Juego de la Vida es un autómata celular bidimensional: en un universo cuadriculado viven unos organismos(representados por un punto en una celda). A estas colonias se les aplican una "leyes genéticas" muy sencillas, de modo que conforme pasa el tiempo la colonia evoluciona pues hay organismos que nacen y otros mueren. Cada celda del universo cuadriculado está rodeada de otras 8 celdas. Las "leyes genéticas" se basan en el número de casillas adyacentes ocupadas. Estas leyes son muy sencillas.
Muchos conocimos el Juego de la Vida por los artículos de Martín Gardner en la revista 'Investigación y Ciencia', posteriormente publicados en libro por Editorial Labor.
Quizás algún lector joven se sienta motivado por este juego y decida, primero, disfrutarlo y, después, programarlo. Es un ejercicio sencillo de programación que tiene muchas posibilidades. Para mí fue uno de los primeros ejercicios cuando aprendía a programar en Pascal y Java. Gracias a Javier Estarán, con el que colaboré en el desarrollo del sitio web 'Artiludios', enteramente en Java. Con la aplicación del Juego de la Vida en Java he generado las animaciones.
Estas son las sencillas leyes del Juego de la Vida de Conway:
Supervivencia
Cada ficha que tenga dos o tres fichas vecinas sobrevivirá en la siguiente generación.
Fallecimiento
Cada ficha que tenga cuatro o más fichas vecinas muere (superpoblación).
Cada ficha con sólo una o ninguna ficha vecina fallece (aislamiento)
Nacimiento
Cada casilla vacía adyacente a, exactamente, tres fichas vecinas es casilla generatriz y en la siguiente generación contiene una ficha.
El Juego de la Vida es un juego de simulación. A partir de una configuración sencilla de organismos se pretende observar la evolución de la colonia aplicándoles las "leyes genéticas" de Conway.
En nuestros ejemplos, el universo en el que viven estas colonias es 'tórico', tiene forma de rosquilla o toro. La parte de la derecha y la izquierda están unidas. También están unidas la parte de arriba y la de abajo.
A pesar de la sencillez de estas leyes, las posibilidades del juego son muchas. Vamos a ver algunas de estas colonias.
Parece claro que habrá colonias que desaparecerán. Otras van a terminar en configuraciones que son estables.
El gato de Cheshire (inspirado en el gato de Cheshire de Alicia en el País de la Maravillas) nos muestra su sonrisa y termina de un modo estable (como una huella de su garra, dice Gardner).
Hay configuraciones periódicas, oscilantes. Recibirán nombres como púlsar, semáforos,....
Estos son dos ejemplos:
Una configuración sencilla y simétrica, llamada PI, evoluciona en una bonita simetría hasta convertirse en 5 osciladores, 6 'bloques' y 2 'lagos'.
Una cuestión interesante es si hay configuraciones que permanecen repitiéndose en el espacio pero trasladándose. Son colonias que viven siempre pero no son estables. Son llamadas deslizadores, naves, naves escoltadas. otras van repitiéndose en el espacio pero trasladándose (deslizadores, naves, naves escoltadas, etc.). Viven siempre
Esta configuración es un convoy formado por una nave grande y dos escoltas medianas:
¿Hay configuraciones que crezcan indefinidamente? La respuesta es que sí. Un buen ejemplo es este cañón generador de deslizadores ligeros.
La siguiente configuración sólo tiene 5 individuos en su origen. Se llama pentómino R. A pesar de su simplicidad evoluciona muchas veces, además de generar deslizadores. En nuestro caso, debido al universo tórico, esos deslizadores colisionarán con los restos de la colonia original.
La cosechadora necesita alimento para deslizarse generando pacas de paja en su trayectoria. Cuando termina de cosechar, queda parada.
REFERENCIAS
Para saber más sobre el Juego de la vida se pueden leer los artículos "El juego de la vida" de Martín Gardner que está incluido en su libro "Ruedas, Vida y otras diversiones matemáticas" (Editorial Labor).
 ANTERIOR
ANTERIOR
MÁS ENLACES













