|
|
|
Complex Functions: Zero and Pole
La función
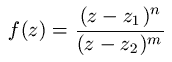
Tiene un cero y un polo. Sus multiplicidades dependen de los exponentes del numerador y del denominador.
En Cero y polo (variante) presentamos otra variante en la que hay más control sobre la representación de estas funciones.
En el caso de que los exponentes sean iguales a 1 es una transformación de Moebius .
Controlando el exponente del numerador y el del denominador de la función modificamos la multiplicidad del cero y del polo.
La multiplicidad del cero o del polo se representa con el número de veces que el ciclo de colores (rojo->verde->azul) aparece en torno al punto.
REFERENCES
Tristan Needham - Visual Complex Analysis. Oxford University Press(pag. 60).
NEXT
PREVIOUS
Every complex polynomial of degree n has n zeros or roots.
MORE LINKS
Complex power functions with natural exponent have a zero (or root) of multiplicity n in the origin.
A polynomial of degree 2 has two zeros or roots. In this representation you can see Cassini ovals and a lemniscate.
A complex polinomial of degree 3 has three roots or zeros.
Every complex polynomial of degree n has n zeros or roots.
Una primera aproximación a estas transformaciones. Representación de dos haces coaxiales de circunferencias ortogonales.
The Complex Exponential Function extends the Real Exponential Function to the complex plane.
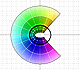
The Complex Cosine Function extends the Real Cosine Function to the complex plane. It is a periodic function that shares several properties with his real ancestor.
The Complex Cosine Function maps horizontal lines to confocal ellipses.
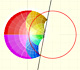
Inversion is a plane transformation that transform straight lines and circles in straight lines and circles.
Inversion preserves the magnitud of angles but the sense is reversed. Orthogonal circles are mapped into orthogonal circles
The usual definition of a function is restrictive. We may broaden the definition of a function to allow f(z) to have many differente values for a single value of z. In this case f is called a many-valued function or a multifunction.
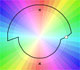
Multifunctions can have more than one branch point. In this page we can see a two-valued multifunction with two branch points.
The complex exponential function is periodic. His power series converges everywhere in the complex plane.
The power series of the Cosine Function converges everywhere in the complex plane.
We will see how Taylor polynomials approximate the function inside its circle of convergence.