Inversion in a circle is a transformation that preserves the magnitude of angles but each angle is mapped to an angle of opposite sign. The sense or direction of each angle is reversed. Inversion in a circle is an anticonformal mapping (like a reflection in a line).

In particular, inversion is a mapping that preserves the angle of intersection of two circles. Orthogonal circles (or lines) invert into orthogonal circles (or lines). A circle orthogonal to the circle of inversion is mapped into itself.

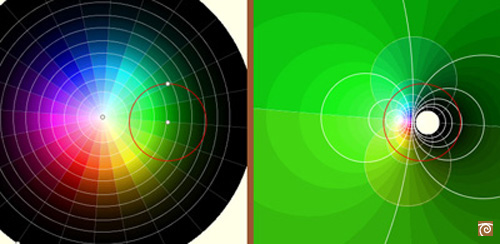
All the lines through a point and all the circles concentric with the same point as a center can be seen as two particular cases of coaxal sistem of circles. These two coaxal sistems are orthogonal. The lines form a coaxal system of intersecting type and the concentric circles are a non-intersecting coaxal system. These coaxal systems are mapped into two orthogonal coaxal systems:

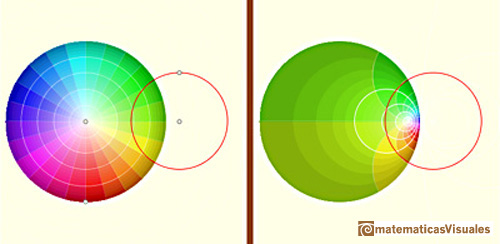
Every "small" rectangle is transformed into an "small" rectangle:

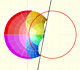
In this picture we can see how the order of colors is reversed:

MORE LINKS

Complex Polynomial Functions(1): Powers with natural exponent

Complex power functions with natural exponent have a zero (or root) of multiplicity n in the origin.

Complex Polynomial Functions(2): Polynomial of degree 2

A polynomial of degree 2 has two zeros or roots. In this representation you can see Cassini ovals and a lemniscate.

Complex Polynomial Functions(3): Polynomial of degree 3

A complex polinomial of degree 3 has three roots or zeros.

Complex Polynomial Functions(4): Polynomial of degree n

Every complex polynomial of degree n has n zeros or roots.

Complex Polynomial Functions(5): Polynomial of degree n (variant)

Every complex polynomial of degree n has n zeros or roots.

Cero and polo (Spanish)

Podemos modificar las multiplicidades del cero y del polo de estas funciones sencillas.

Cero and polo (variant) (Spanish)

The Complex Exponential Function

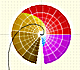
The Complex Exponential Function extends the Real Exponential Function to the complex plane.

The Complex Cosine Function

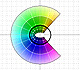
The Complex Cosine Function extends the Real Cosine Function to the complex plane. It is a periodic function that shares several properties with his real ancestor.

The Complex Cosine Function: mapping an horizontal line

The Complex Cosine Function maps horizontal lines to confocal ellipses.

Multifunctions: Two branch points

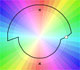
Multifunctions can have more than one branch point. In this page we can see a two-valued multifunction with two branch points.

Taylor polynomials: Complex Exponential Function

The complex exponential function is periodic. His power series converges everywhere in the complex plane.

Taylor polynomials: Complex Cosine Function

The power series of the Cosine Function converges everywhere in the complex plane.

Taylor polynomials: Rational function with two complex singularities

We will see how Taylor polynomials approximate the function inside its circle of convergence.