Matematicas Visuales | Normal distributions: Calculating probabilities

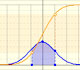
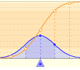
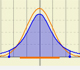
It may be interesting to familiarize ourselves with the probabilities correspondig to different intervals in normal distributions.

Probability for an Interval = Area under the density curve in that interval

On the basis of a probability density function, you can calculate the probability that the random variable falls within a given range by estimating the area under the curve for that range. With the cumulative probability function you can do the same, but then more accurately

Two points on the x-axis determine the extremes of the interval for which the probability is calculated (approximately)

Different options A1, A2, ..., A6 correspond to different intervals that can be defined with those two points. Taken in pairs these are complementary in the sense that the sum of probabilities is 1.

We can modify the parameters of the normal distribution and see how the probabilities vary.

The red dots control vertical and horizontal scales of the graphic.

REFERENCES

George Marsaglia's article Evaluating the Normal Distribution.

next NEXT

Normal Distributions: Probability of Symmetric Intervals

Calculating probabilities of symmetric intervals around the mean of a normal distribution.

Normal Distributions: One, two and three standard deviations

One important property of normal distributions is that if we consider intervals centered on the mean and a certain extent proportional to the standard deviation, the probability of these intervals is constant regardless of the mean and standard deviation of the normal distribution considered.

MORE LINKS

Student's t-distributions

Student's t-distributions were studied by William Gosset(1876-1937) when working with small samples.

Calculating probabilities in t Student distributions (Spanish)

Binomial distribution

When modeling a situation where there are n independent trials with a constant probability p of success in each test we use a binomial distribution.

Normal approximation to Binomial distribution

In some cases, a Binomial distribution can be approximated by a Normal distribution with the same mean and variance.

Normal distributions

The Normal distribution was studied by Gauss. This is a continuous random variable (the variable can take any real value). The density function is shaped like a bell.

Poisson distribution

Poisson distribution is discrete (like the binomial) because the values that can take the random variable are natural numbers, although in the Poisson distribution all the possible cases are theoretically infinite.