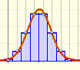
Las distribuciones t de Student son parecidas a la normal. Se pueden utilizar para hacer estimaciones de la media cuando se desconoce la varianza (es lo habitual) y se usan muestas pequeñas.
Los intervalos así obtenidos son, no podría ser de otra manera, más grandes y menos precisos que los que se obtendrían si supusieramos conocida la varianza en una distribución normal.
En el vídeo comparamos distribuciones t de Student con la normal estándar. Podemos elegir el valor del parámetro "grados de libertad" y modificar los extremos del intervalo simétrico en torno a la media. Con estos datos se obtiene unas probabilidades (cálculos aproximados) que se muestran. A1 representa el área de la zona central y A2 es el área de las dos colas de los extremos. La suma de ambas áreas es 1.
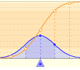
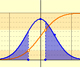
Si consideramos esos mismos extremos del intervalo en el caso de una distribución normal estándar comprobamos que la probabilidad de la zona central (A1) es mayor para la distribución normal que para la t de Student. Si el parámetro grados de libertad es grande la diferencia es pequeña.
Partiendo de un intervalo podemos obtener una probabilidad en una distribución t de Student. Nos podemos plantear el tamaño del intervalo que barre la misma área bajo la campana de Gauss. El extremo positivo del intervalo se calcula y se muestra en "x1 Normal". El segmento dibujado de color naranja debajo de las gráficas representa ese intervalo que es de menor amplitud que el correspondiente de la t de Student. Podemos ver cómo si el parámetro grados de libertad es suficientemente grande la diferencia entre ambos intervalos es pequeña.
Los puntos grises controlan la escala vertical y horizontal de la gráfica y pulsando el boton derecho y arrastrando podemos moverla a derecha e izquierda.
LINKS