En casa: Plegado de un tetraedro (origami modular)
Hemos visto que es sencillo plegar un triángulo equilátero.

Con unos sencillos pliegues podemos doblar un triángulo equilátero. ¿Sabrías demostrar que los ángulos son de 30º y de 60º?.
Vamos a utilizar esta técnica para construir un tetraedro de origami modular.
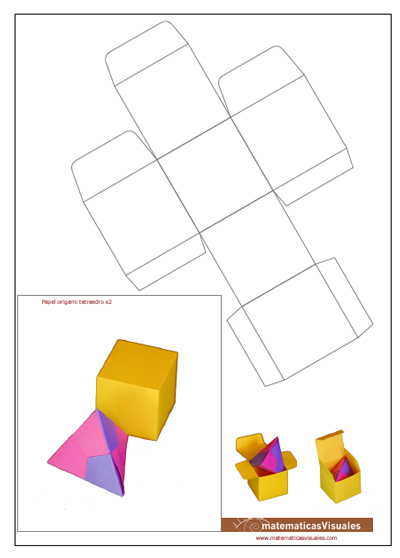
Con origami construiremos un tetraedro que podremos poner dentro de una cajita cúbica hecha con cartulina.
Este será el resultado:
Los dos primeros dobleces se muestran en la siguiente imagen. ¿Podemos justificar que el doblez es medio triángulo
equilátero?
Los pendientes son un regalo de la profesora Inmaculada Ordóñez Ríos. Ella fue quién me enseñó amablemente a
plegar esta figura.
Estas son las instrucciones para el plegado del tetraedro con origami modular. Se tienen que doblar dos módulos a partir de
dos rectángulos de papel (preferiblemente de dos colores). La dificultad principal consiste en ver que los dos módulos no son
iguales sino simétricos. Hay que comprobar esto pues si los dos son iguales no se monta la figura.
Como un interesante complemento proponemos la construcción de una cajita cúbica.
Este es el modelo de la caja cúbica que se pueden descargar. El rectángulo es el tamaño de papel que necesitamos para el plegado de un
tetraedro que cabe perfectamente en la caja:
¿Te animas a hacer esta construcción del tetraedro de origami?
Enviar una fotografía a
mi contacto para su publicación.
Contacto para dudas, comentarios, enviar fotos con construcciones matemáticas o respuestas.
Otra construcción de un tetraedro inscrito en un cubo se puede hacer con pajitas:

Una manera muy elegante de dar rigidez al cubo es construir un tetraedro dentro del cubo. A partir de un cubo se pueden construir dos tetradros distintos de este modo.
En la siguiente variante he plegado dos tetraedros, uno en papel y otro con acetato para mostrar que el
tetraedro es un poliedro dual de sí mismo (o autodual).
También se pueden construir octaedros y, con paciencia, montar esta estructura fractal.
Fíjate que lo que una cosa que nos enseña esta figura es que dentro del tetraedro hay un octaedro. El tetraedro se puede ver como
un octaedro al que se le han añadido 4 tetraedros en 4 de sus caras.
Todas estas construcciones nos enseñan propiedades de estos poliedros. En particular, a partir de ellas se puede calcular con
facilidad el volumen del tetraedro.
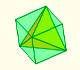
Podemos inscribir un tetraedro en un cubo. A partir de esta construcción calculamos el volumen de un tetraedro.
 ANTERIOR
ANTERIOR

Página con enlaces de actividades matemáticas que podemos hacer en casa.
MÁS ENLACES

Página con enlaces de actividades matemáticas que podemos hacer en casa sencillas. Pensadas para alumnops de edad aproximada 9-13 años.

Página con enlaces de actividades matemáticas fáciles que podemos hacer en casa. Pensadas para alumnos de Educación Secundaria, edad aproximada 12-16 años.

Página con enlaces de actividades matemáticas que podemos hacer en casa un poco más complicadas. Pensadas para alumnos de Bachillerato o último año de Educación Secundaria. Edad aproximada, a partir de 15 años.

Ejercicios de cálculo mental en el que se practican algunas estructuras básicas con el propósito de mejorar la seguridad y autoconfianza.

Si tenemos impresora en casa podemos imprimir plantillas en cartulina (o papel) y hacer interesantes construcciones. Muchas son sencillas y puedes intentar hacerlas con reglas y compás. Aunque no puedas hacerlas, también puedes mirarlas pues de ellas sacaremos interesantes consecuencias matemáticas.

El Concurso de Primavera de Matemáticas es organizado por la Asociación Matemática Concurso de Primavera y la Facultad de Matemática de la UCM. Sus problemas están pensados para que sean agradables.

En casa se actualiza, por lo menos, 5 veces a la semana mientras dura el confinamiento. Aquí se puede ver la sucesión cronológica de las publicaciones.

Contacto para dudas, comentarios, enviar fotos con construcciones matemáticas o respuestas.

La representación gráfica de datos nos muestra los datos de un modo visual e intuitivo. Se muestran ejemplos en relación con el estudiio de las visitas al sitio matemátivasVisuales.















 ANTERIOR
ANTERIOR