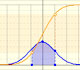
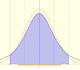
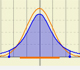
En algunos casos una Distributión Binomial puede aproximarse por una Distributión Normal (que tenga la misma media y varianza).
Si X es una variable aleatoria con una Distribución Normal podemos escribir:
Entonces, si Y es una variable aleatoria Normal con la misma media y varianza:
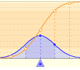
Podemos usar dos aproximaciones de la Normal a la Binomial. En primer lugar, podemos usar la función de densidad normal como una aproximación de la binomial. En el applet, esta aproximación está representada por la línea naranja.
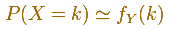
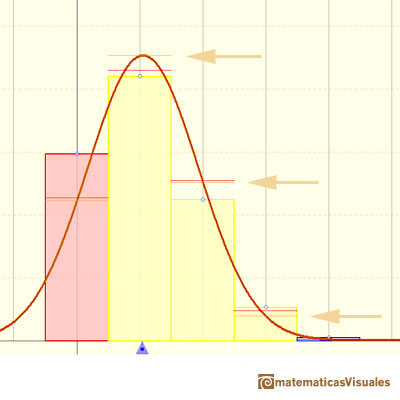
Una segunda aproximación es mejor y más práctica si usamos las tablas de la Distribución Normal. En este caso usamos una corrección de continuidad, como en este ejemplo:
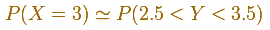
En el applet, esta aproximación se corresponde con la línea roja.
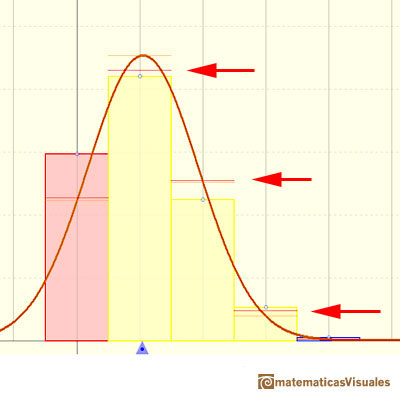
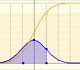
En el applet queremos representar intuitivamente cómo en algunos casos la aproximación no es aceptable y en otros es buena. Cuando el error absoluto de la aproximación normal es menor que 0.005 dibujamos un rectángulo azul. Si la aproximación está entre 0.005 y 0.05 dibujamos un rectángulo amarillo y si la aproximación es menos precisa el rectángulo es rojo.
Aquí podemos ver un caso en el que la aproximación parece precisa:
En este caso la aproximación no es tan precisa:
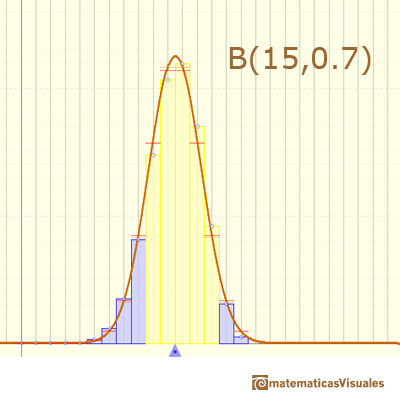
Y en el siguiente caso la paroximación es mala:
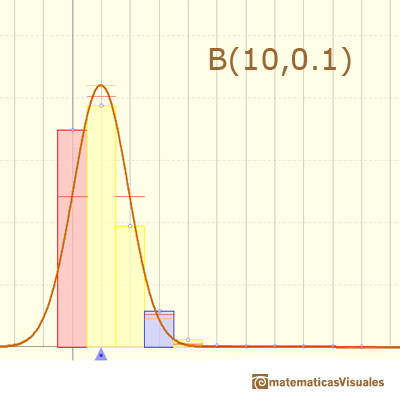
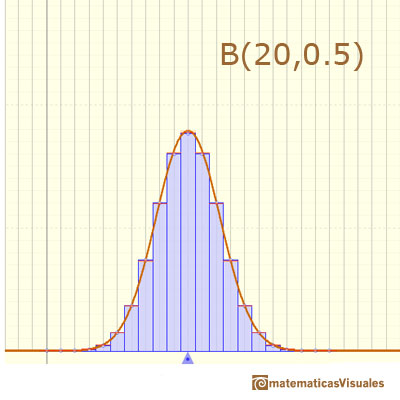
En el applet podemos cambiar el parámetro n.
La media está representada por un triángulo azul y puede verse como el punto de equilibrio. Arrastrándolo con el ratón modificamos el parámetro p.
Cambiando estos dos parámetros podemos ver como cambia la precisión en la aproximación de la distribución Binomial por la Normal.
Los puntos rojos controlan las escalas vertical y horizontal.
Si n es "bastante grande" y p está "próximo a" 0.5, la distribución será bastante simétrica y parecida a la Normal. En estos casos, la Distribución Normal puede darnos excelentes aproximaciones. Sin embargo, la aproximación no será precisa para valores pequeños de n. Hay varias reglas o criterios que intentan precisar cuando es adecuado el uso de la aproximación Normal (aunque esto depende del problema estudiado y de la conveniencia de una mayor o menor precisión). Por ejemplo, una regla dice que podemos usar la aproximación Normal sólo si
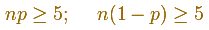
La aproximación generalmente mejora si n crece y es mejor cuando p no está cerca de 0 o de 1.
Aquí podemos ver un ejemplo típico que representa el uso de las tablas de la Distribución Normal para calcular probabilidades en una Distribución Binomial (usando la corrección de continuidad).
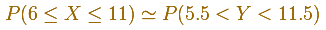
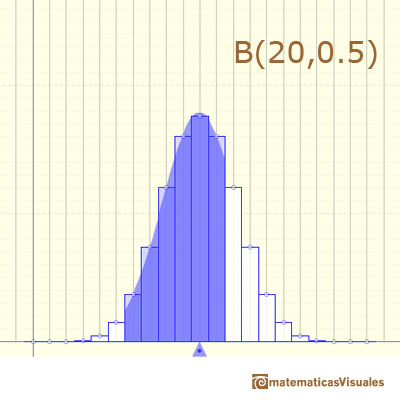
Cuando n es grande los cálculos exactos de probabilidades con la Distribución Binomial pueden ser muy largos, pero usando las tablas de la Distribución Normal estos cálculos son sencillos. Históricamente éste fue el primer uso de la Distribución Normal y fue introducido por Abraham de Moivre.
REFERENCIAS
 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR
MÁS ENLACES