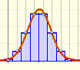
Usando la función de distribución (acumulada) podemos calcular la probabilidad de cualquier intervalo:
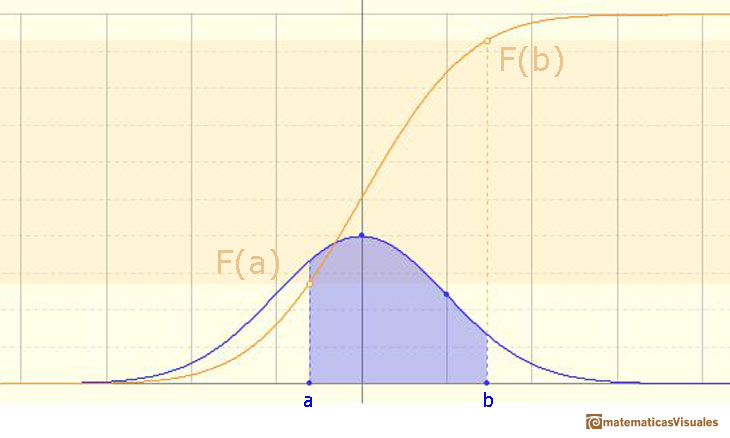
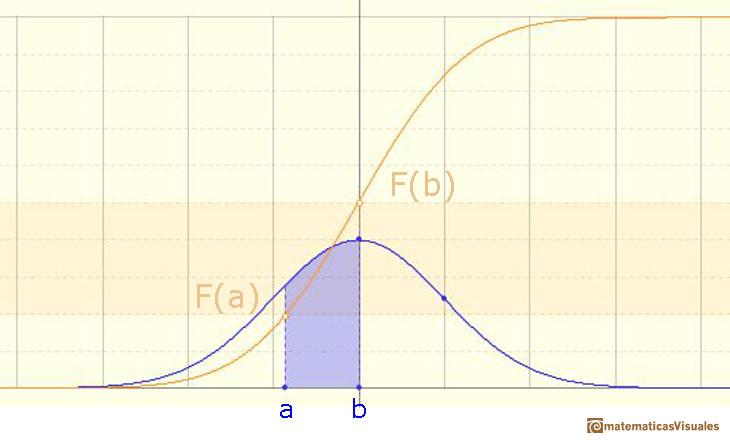
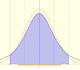
En esta página vamos a estudiar un caso particular simple pero muy interesante: intervalos simétricos alrededor de la media.
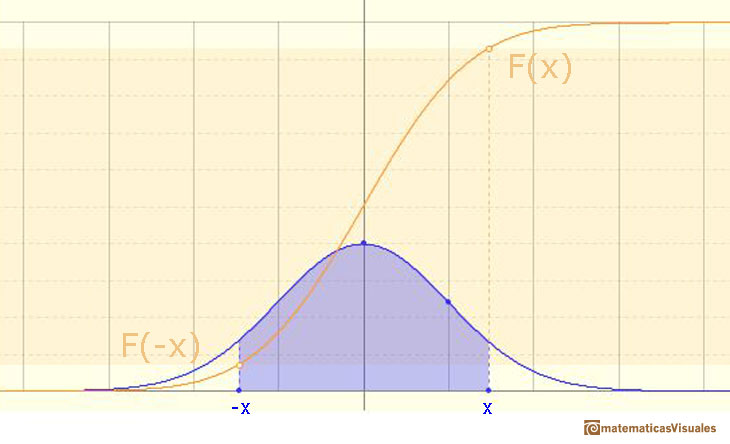
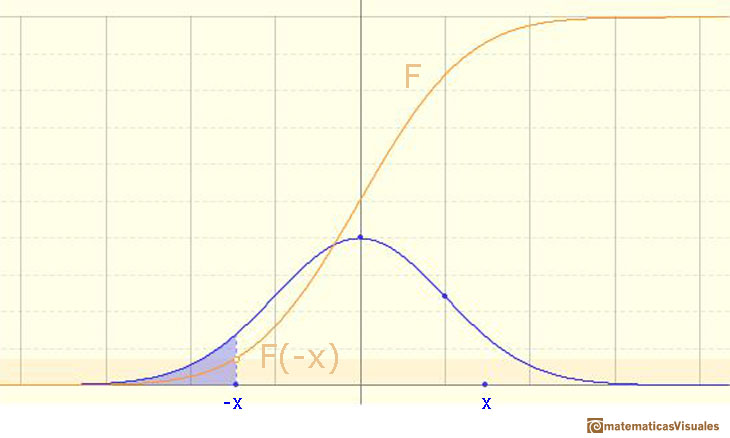
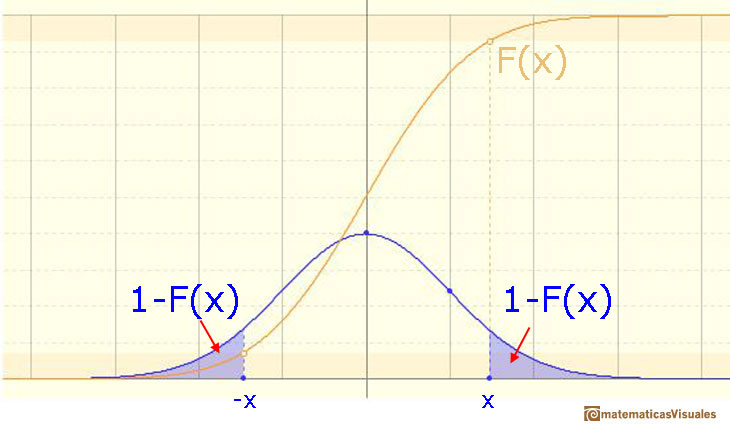
Then
Podemos modificar los parámetros de la distribución normal.
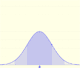
La media está representada por un triángulo y se puede interpretar como un punto de equilibrio. Al arrastrarlo se modifica la media.
Arrastrando el punto sobre la curva (que es uno de los dos puntos de inflexión de la curva) se modifica la desviación típica.
El punto azul sobre el eje X representa el valor x de la variable. Al moverlo modificamos el intervalo simétrico.
Podemos ver la función de distribución (acumulada) y cómo cambia cuando modificamos la media (una simple traslacion) y la desviación típica (reflejando una mayor o menor dispersión de la variable).
Los puntos rojos controlan la escala vertical y horizontal de la gráfica.
REFERENCIAS
 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR
MÁS ENLACES