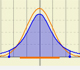
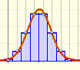
Cálculo de probabilidades en distribuciones normales

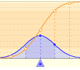
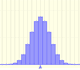
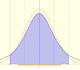
Dos puntos en el eje de abcisas determinan los diferentes intervalos de los que se calculan (aproximadamente) las probabilidades.

Las diferentes opciones A1, A2, ..., A6 se corresponden con diferentes intervalos que se pueden definir con esos dos puntos. Tomados por parejas son complementarios en el sentido de que la suma de las probabilidades es 1, es decir, el total.

Podemos modificar los parámetros de la distribución normal y comprobar cómo varían las probabilidades.

Los puntos grises controlan la escala vertical y horizontal de la gráfica y pulsando el boton derecho y arrastrando podemos moverla a derecha e izquierda.

ENLACES

	Distribución Normal La distribución normal fue estudiada por Gauss.
	Una, dos y tres desviaciones típicas Propiedad de las distribuciones normales.