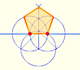
|
|
|
In this page we are going to see two ways to draw a 15º angle with a ruler and a 'rusty' compass (a compass of fixed opening). These are very simple constructions and there are, of course, many other ways to do the same (bisecting a 60º angle, subtracting 45º from 60º, ...).
They are basic examples of application of the properties of the angles central and inscribed in a circle (although, as we are going to see later, we can use more basic arguments involving some isosceles triangles).
The first construction is straightforward, and the result is very easy to see as a simple case of the property of angles central and inscribed in a circle:
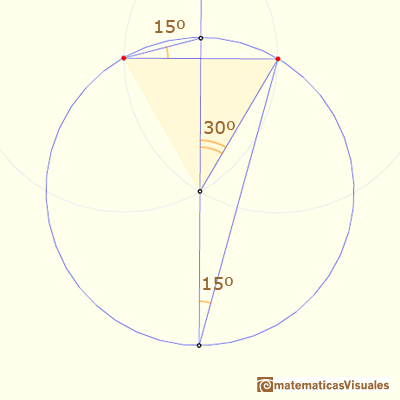
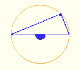
Another basic approach follows. In the next image, the triangle CBO is an isosceles triangle, then:
And we can calculate the angle:
Now we are going to see a second construction of a 15º angle:
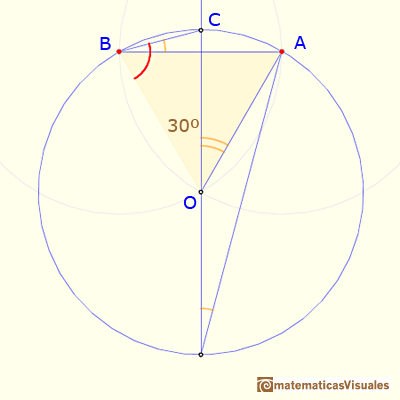
Again it is an example of the property of the angles central and inscribed in a circle:
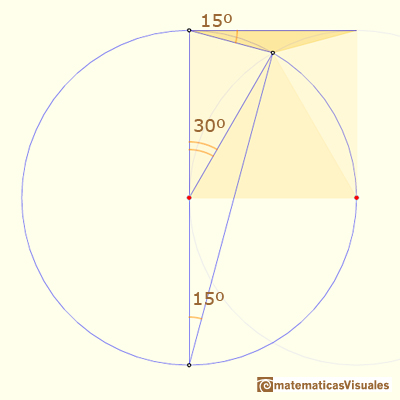
In the next image, we can see that the triangle CB0 is an isosceles triangle, then:
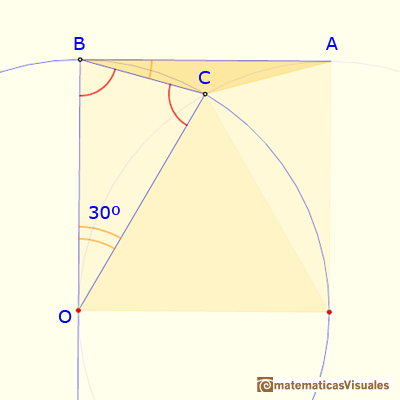
To finish, we can calculate the angle:
NEXT
PREVIOUS
MORE LINKS
