Ángulo central e inscrito en una circunferencia: Caso II
Teorema del Ängulo central: El ángulo central es el doble del ángulo en la circunferencia.
CASO 2. Cuando una de las cuerdas que forman el ángulo inscrito es un diámetro.
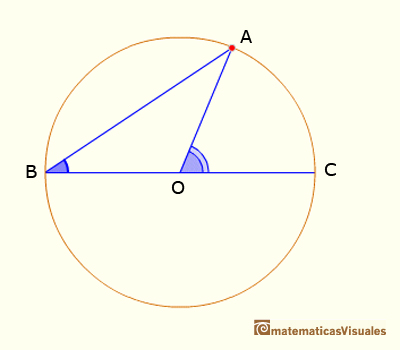
En este caso queremos probar que:
Dibujamos la línea OP paralela a AB y entonces
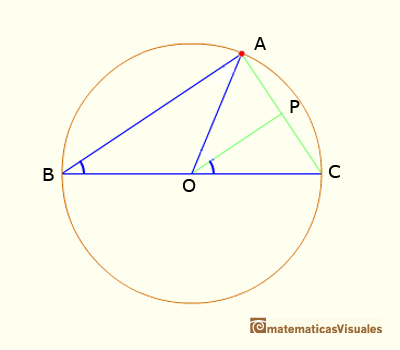
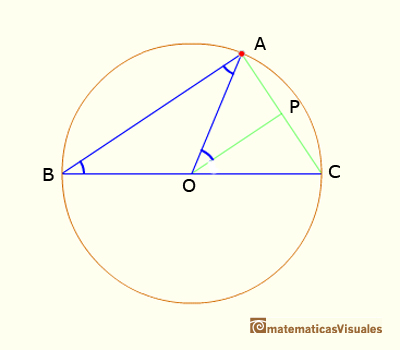
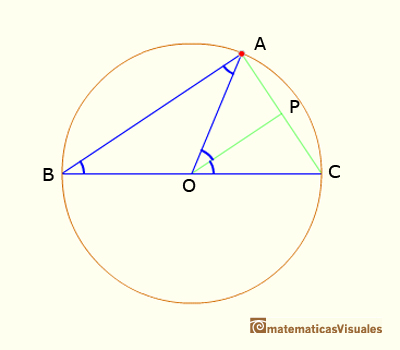
Sumando estos dos ángulos obtenemos el resultado
Ahora es fácil probar el caso general. Podemos ver una demostración interactiva de la propiedad de los ángulos central e inscrito en una circunferencia| Caso General.
REFERENCIAS
Los Elementos de Euclides
SIGUIENTE
Demostración interactiva de la propiedad de los ángulos central e inscrito en una circunferencia. Prueba del caso general.
ANTERIOR
Demostración interactiva de la propiedad de los ángulos central e inscrito en una circunferencia. Caso I: Cuando el arco es una semicircunferencia el ángulo inscrito es recto.
MÁS ENLACES
Teorema del Ängulo central: El ángulo central es el doble del ángulo en la circunferencia.
Usando regla y compás podemos dibujar ángulos de 15 grados. Son ejemplos básicos de las propiedades de los ángulos central e inscrito en una circunferencia.
Demostración dinámica e interactiva del teorema de Pitágoras, inspirada en la de Euclides.
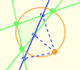
A partir de cada punto de la circunferencia circunscrita a un triángulo se obtiene una recta llamada recta de Simson-Wallace o recta de Simson.
Demostración interactiva de que los tres puntos que determinan cada recta de Wallace-Simson están alineados.
Podemos dibujar un pentágono regular dado uno de sus lados construyendo la razón áurea con regla y compás.
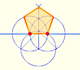
En su libro 'Underweysung der Messung' Durero dibujó un pentágono no regular con regla y compás con apertura fija. Es una construcción simple y una muy buena aproximación de un pentágono regular.
La diagonal y el lado de un pentágono regular están en proporción áurea. El punto de intersección de dos diagonales de un pentágono regular divide a ambas en la razón áurea o 'en razón extrema y media'.