En esta página vamos a ver dos maneras de dibujar un ángulo de 15º usando una regla y un compás 'oxidado' (un compás con la apertura fija). Son construcciones muy simples y hay otras maneras de dibujar estos ángulos (haciendo la bisectriz de un ángulo de 60º, restando 45º de 60º, etc.)

Podemos justificar estas construcciones como aplicaciones sencillas e las propiedades de los ángulos central e inscrito en una circunferencia (aunque, como veremos después, se pueden usar argumentos todavía más básicos referidos a triángulos isósceles).

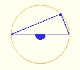
La primera construcción se hace muy rápido y es un caso elemental de la propiedad de los ángulos central e inscrito en una circunferencia.

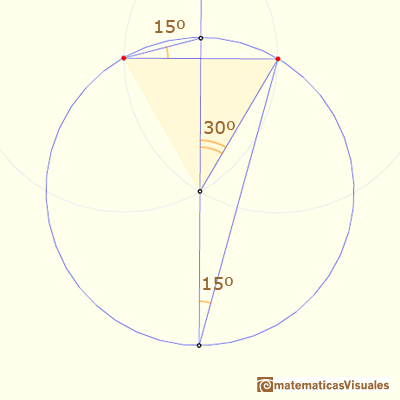
Otra manera de justificar la construcción es usando triángulos equiláteros. En la siguiente imagen, el triángulo CBO es una triángulo isósceles, entonces:

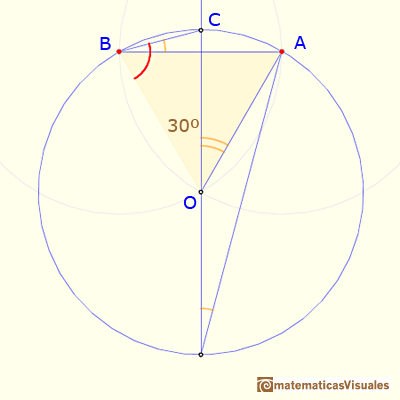
Podemos calcular el ángulo:

Ahora vamos a ver una segunda construcción del ángulo de 15º:

También es un ejemplo de la propiedad de los ángulos central e inscrito en una circunferencia (ahora en relación con la recta tangente):

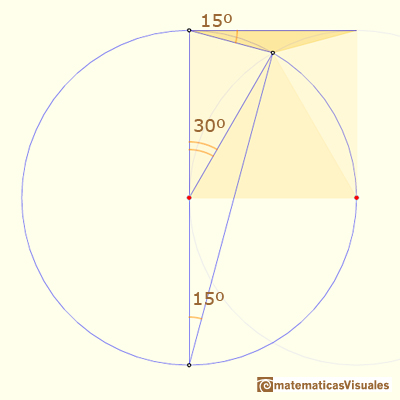
En la siguiente imagen podemos ver que el triángulo CBO es un triángulo isósceles, entonces:

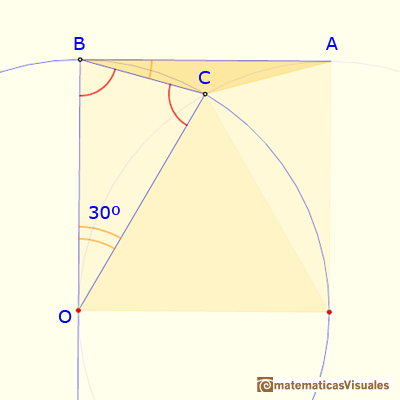
Para terminar, podemos calcular el ángulo:

MÁS ENLACES

Ángulos central e inscrito en una circunferencia | Demostración | Caso II

Demostración interactiva de la propiedad de los ángulos central e inscrito en una circunferencia. Caso II: Cuando una cuerda de las que forman el ángulo inscrito es un diámetro.

Ángulos central e inscrito en una circunferencia | Demostración | Caso General

Demostración interactiva de la propiedad de los ángulos central e inscrito en una circunferencia. Prueba del caso general.

Rectas de Simson-Wallace

A partir de cada punto de la circunferencia circunscrita a un triángulo se obtiene una recta llamada recta de Simson-Wallace o recta de Simson.

Rectas de Wallace-Simson | Demostración

Demostración interactiva de que los tres puntos que determinan cada recta de Wallace-Simson están alineados.

Dibujo de un pentágono regular con regla y compás

Podemos dibujar un pentágono regular dado uno de sus lados construyendo la razón áurea con regla y compás.

Aproximación de Durero de un pentágono regular

En su libro 'Underweysung der Messung' Durero dibujó un pentágono no regular con regla y compás con apertura fija. Es una construcción simple y una muy buena aproximación de un pentágono regular.

La diagonal de un pentágono regular y la razón áurea

La diagonal y el lado de un pentágono regular están en proporción áurea. El punto de intersección de dos diagonales de un pentágono regular divide a ambas en la razón áurea o 'en razón extrema y media'.