Los tres puntos de intersección de las trisectrices adyacentes de los ángulos de un triángulo cualquiera son los vértices de un triángulo equilátero.
Este triángulo equilátero se llama triángulo de Morley.
Este sorprendente descubrimiento se debe a Frank Morley (en torno a 1900).
Empezamos con un triángulo cualquiera y trisecamos cada uno de sus ángulos (los dividimos en tres partes iguales)...
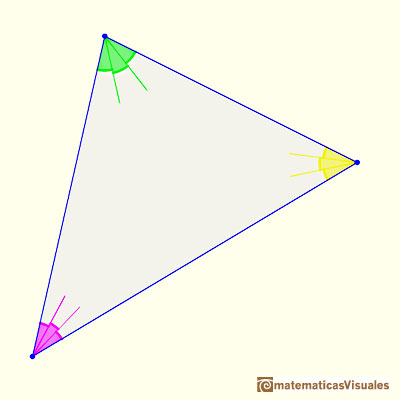
Extendemos esas trisectrices ...
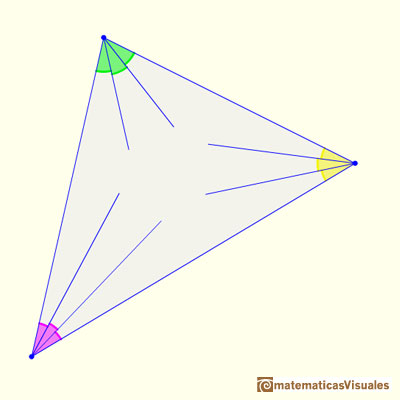
Consideramos los tres puntos de intersección de las trisectrices adyacentes ...
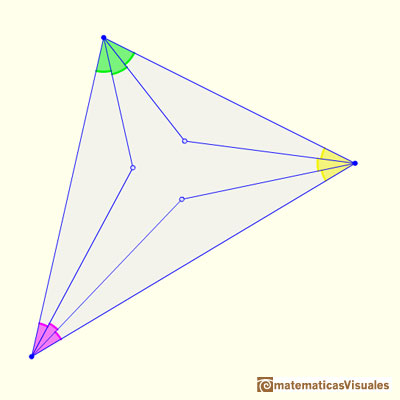
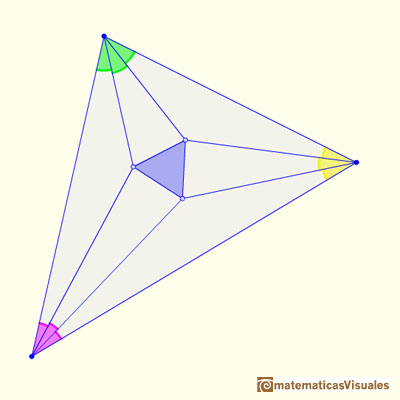
Y siempre obtenemos un triángulo equilátero llamado triángulo de Morley. Esto ocurre para cualquier triángulo.
Podemos ver un vídeo inspirado en la prueba que hace John Conway del teorema de Morley. Una demostración "de atrás para adelante" muy bonita.
Demostración muy bonita y visual de Conway. Podemos jugar con una animación interactiva y ver los diferentes pasos de la demostración.
REFERENCIAS
Coxeter, H. S. M. and Greitzer, S. L. Geometry Revisited. Washington, DC: Math. Assoc. Amer.
Coxeter, H. S. M. Introduction to Geometry, 2nd ed. New York: John Wiley and sons, 1969.
John Conway. On Morley's Trisector Theorem, The Mathematical Intelligencer, 2014.
John Conway. The Power of Mathematics.
MÁS ENLACES
El triángulo equilátero determinado por la deltoide de Steiner tiene los lados paralelos al triángulo de Morley pero con orientación opuesta.
A partir de cada punto de la circunferencia circunscrita a un triángulo se obtiene una recta llamada recta de Simson-Wallace o recta de Simson.
Demostración interactiva de que los tres puntos que determinan cada recta de Wallace-Simson están alineados.
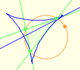
La envolvente de las rectas de Simson-Wallace de un triángulo es una curva con tres cúspides que se llama Deltoide de Steiner.
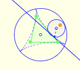
La construcción de la deltoide de Steiner como hipocicloide está relacionada con la circunferencia de los nueve puntos.
Teorema del Ängulo central: El ángulo central es el doble del ángulo en la circunferencia.
SIGUIENTE