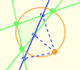
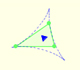
Ya hemos visto que Jacob Steiner (1796-1863) probó que la envolvente de las rectas de Wallace-Simson de un triángulo es una curva que tiene tres cúspides que se llama Deltoide de Steiner.

Deltoide de Steiner

La envolvente de las rectas de Simson-Wallace de un triángulo es una curva con tres cúspides que se llama Deltoide de Steiner.

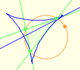
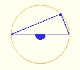
Por otra parte, un deltoide es una curva específica de la familia de las curvas hipocicloides. Una hipocicloide es una curva plana generada por la traza de un punto fijo en una circunferencia pequeña que rueda sin deslizarse por dentro de una circunferencia más grande. El deltoide se genenera cuando el radio de la circunferencia que gira es un tercio del radio de la circunferencia exterior.

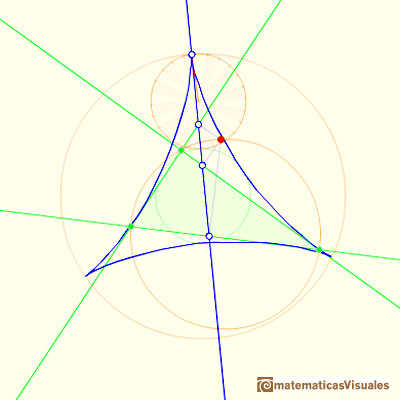
En esta página exploramos el hecho de que el deltoide de Steiner es hipocicloide, es decir que está generada por una circunferencia rodando dentro de otra.

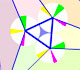
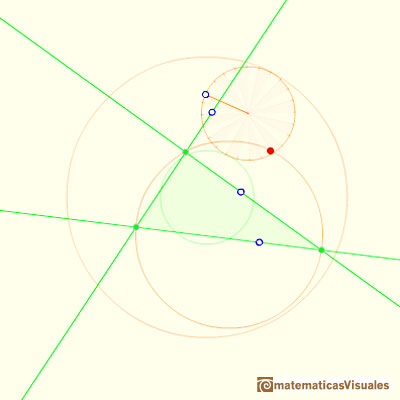
Ambas circunferencias están relacionadas con la circunferencia de Feuerbach o circunferencia de los nueve puntos (es la circunferencia verde en la imagen). El radio de la circunferencia de los nueve puntos es la mitad del radio de la circunferencia circunscrita al triángulo. La circunferencia exterior tiene el mismo centro que la circunferncia de los nueve puntos y su radio es tres veces el radio de la circunferencia de los nueve puntos.

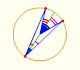
La circunferencia pequeña que rueda tiene el mismo radio que la circunferencia de Feuerbach y ambas son tangentes.

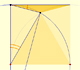
Cuando la circunferencia pequeña rueda sin deslizarse genera el deltoide de Steiner.

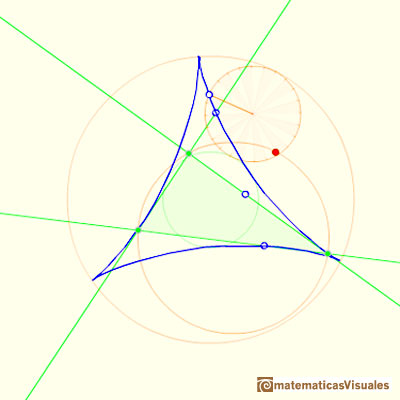
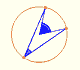
El deltoide de Steiner es tangente a la circunferencia de los nueve puntos.

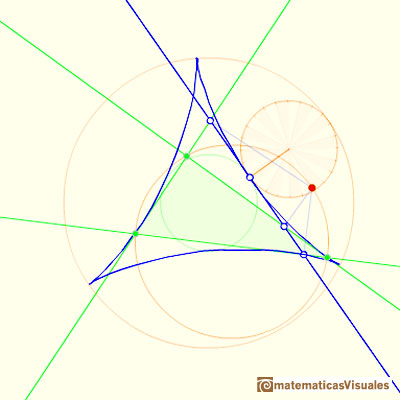
Las tres tangentes al deltoide en las tres cúspides del deltoide concurren en un punto: el centro de la circunferencia de los nueve puntos.

MÁS ENLACES

Rectas de Simson-Wallace

A partir de cada punto de la circunferencia circunscrita a un triángulo se obtiene una recta llamada recta de Simson-Wallace o recta de Simson.

Rectas de Wallace-Simson | Demostración

Demostración interactiva de que los tres puntos que determinan cada recta de Wallace-Simson están alineados.

Ángulos central e inscrito en una circunferencia

Teorema del Ängulo central: El ángulo central es el doble del ángulo en la circunferencia.

Ángulos central e inscrito en una circunferencia | Demostración | Caso I

Demostración interactiva de la propiedad de los ángulos central e inscrito en una circunferencia. Caso I: Cuando el arco es una semicircunferencia el ángulo inscrito es recto.

Ángulos central e inscrito en una circunferencia | Demostración | Caso II

Demostración interactiva de la propiedad de los ángulos central e inscrito en una circunferencia. Caso II: Cuando una cuerda de las que forman el ángulo inscrito es un diámetro.

Ángulos central e inscrito en una circunferencia | Demostración | Caso General

Demostración interactiva de la propiedad de los ángulos central e inscrito en una circunferencia. Prueba del caso general.

Dibujando ángulos de quince grados con regla y compás

Usando regla y compás podemos dibujar ángulos de 15 grados. Son ejemplos básicos de las propiedades de los ángulos central e inscrito en una circunferencia.

Teorema de Morley

Los tres puntos de intersección de las trisectrices adyacentes de los ángulos de un triángulo cualquiera son los vértices de un triángulo equilátero (Triángulo de Morley).

Demostración de John Conway del teorema de Morley

Demostración muy bonita y visual de Conway. Podemos jugar con una animación interactiva y ver los diferentes pasos de la demostración.