Ha muerto el matemático John Conway, inventor del Juego de la Vida y, entre otras muchas cosas, autor de esta demostración preciosa del teorema de Morley.
En el siguiente enlace se presenta el Juego de la Vida:

En esta página podemos jugar con una animación interactiva sobre la demostración de John Conway del teorema de Morley.
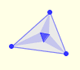
Este teorema fue un sorprendente descubrimiento que hizo Frank Morley (hacia 1899).
Conway escribe: "El teorema de Morley es reconocido como un teorema que es realmente difícil de probar. Es muy sencillo de formular, pero muy difícil de probar"(John Conway).
Se considera que la demostración de John Conway es la más sencilla y es un buen ejemplo de "demostración de atrás para adelante".
"Podemos probar el teorema de Morley de un modo sencillo como sigue. Primero, tienen que decirme la medida de los tres ángulos A, B, C, de su triángulo original. Recordamos que tienen que sumar 180 grados. Este es el plan: Voy a empezar con un triángulo equilátero de algún tamaño
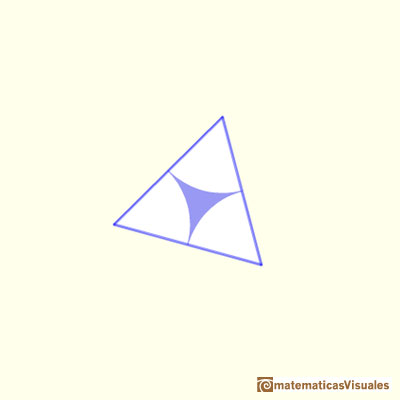
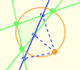
y vamos a construir otros seis triángulos alrededor de él y los vamos a pegar juntos para crear un triángulo cuyos ángulos son A, B y C, justamente igual que los suyos; por lo tanto, para algún tamaño adecuado del triángulo equilátero, mi construcción reproducirá exactamente su triángulo original; además el método de construcción probará que si trisecamos los ángulos de su triángulo encontraremos un triángulo equilátero en el medio. Estas son las seis piezas triangulares que construiremos alrededor del triángulo equilátero" (John Conway)
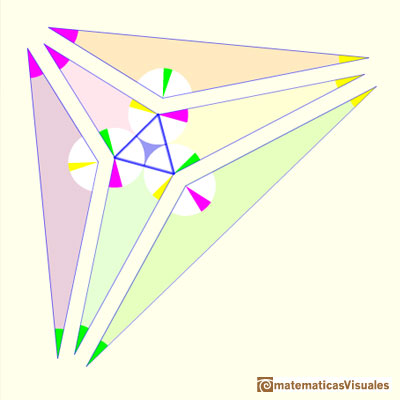
"Para entender la demostración correctamente, tenemos que pensar los seis nuevos triángulos como piezas que vamos a definir, empezando por el triángulo equilátero, con la ayuda de los valores A, B y C iniciales. La figura anterior es nuestro destino, no el punto de partida.
Construiremos los seis nuevos triángulos primero definiendo su forma y después definiremos su tamaño. Para definir las formas de estos seis triángulos tenemos que fijar sus ángulos." (John Conway)
Los ángulos blancos miden 60 grados. Podemos comprobar que los ángulos de cada triángulo suman 180 grados.
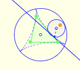
Estas son las formas de los primeros tres triángulos:
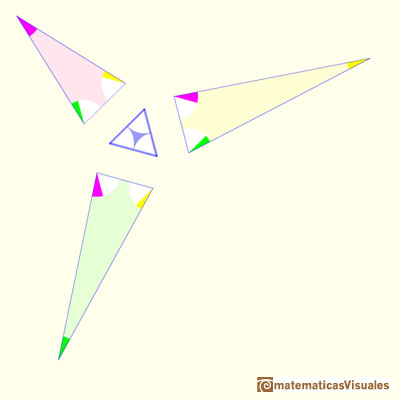
Para fijar los tamaños de estos tres triángulos hacemos que la longitud de uno de los lados sea igual a la del triángulo equilátero.
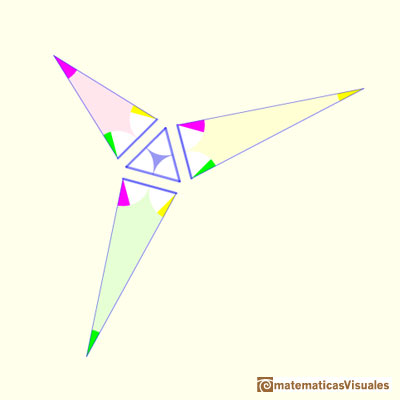
Podemos pegar estos tres triángulos al triángulo equilátero:
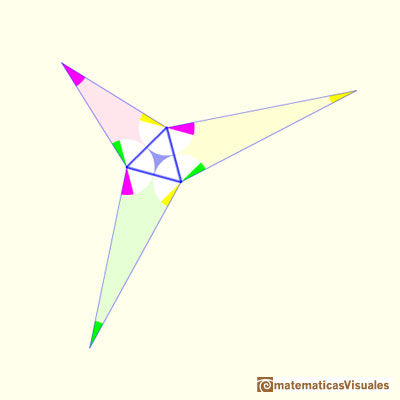
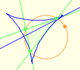
Para fijar las tamaños de los tres triángulos obtusos introducimos dos segmentos iguales desde el vértice opuesto al lado largo de cada triángulo ("un poco al estilo como si trazáramos perpendiculares", escribe Conway). Estas líneas forman triángulos isósceles.
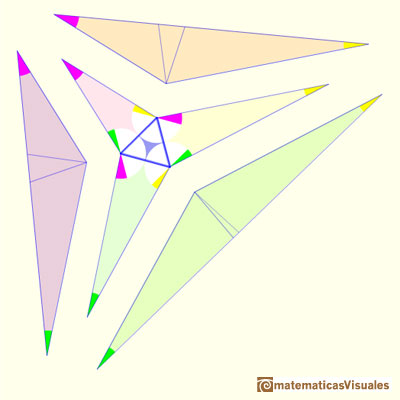
Podemos fijar el tamaño de estos triángulos haciendo que estos segmentos tengan la misma longitud que el lado del triángulo equilátero.
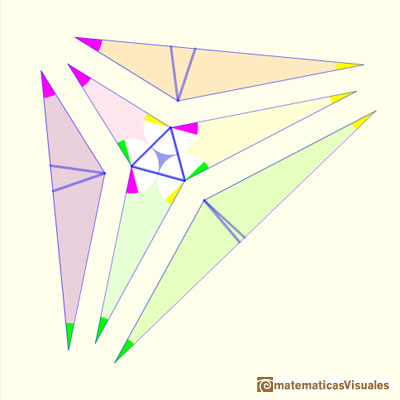
Pero ¿cómo se dibujan estos segmentos? Mirando las figuras podemos entender los ángulos que se forman.
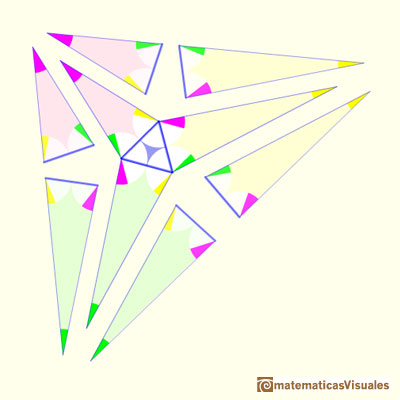
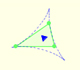
Desdoblando esos tres triángulos obtenemos seis triángulos. Por parejas son iguales a uno de los tres triángulos que construímos primero. Es decir, de los nueve triángulos que tenemos alrededor del equilátero, los tres que comparten el color son iguales (o quizás imágenes especulares). Nos fijamos que tienen tres ángulos iguales y también tienen igual un lado (que es igual al lado del triángulo equilátero).

Podemos comprobar que las medidas de los ángulos son correctas y que los ángulos alrededor de cada vértice interno suman 360 grados.
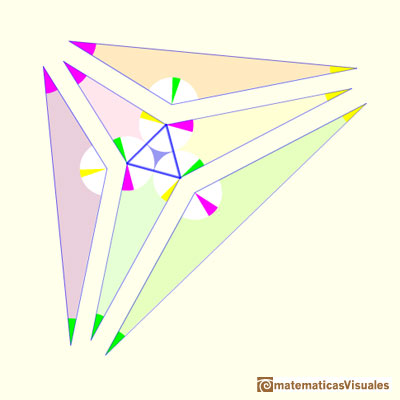
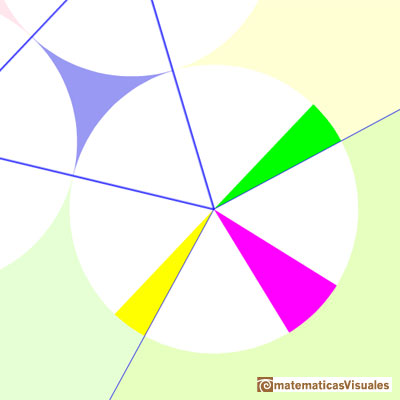
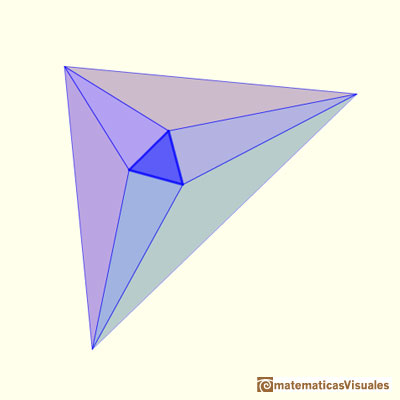
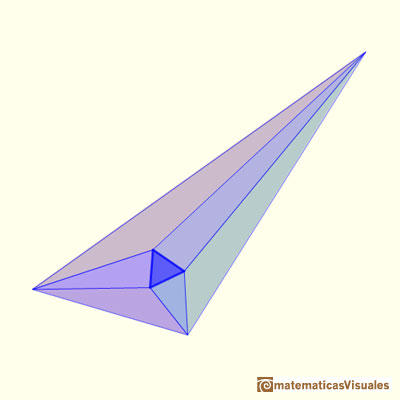
"Entonces, pegando las siete piezas juntas he conseguido un triángulo con los ángulos que usted me ha proporcionado, para el que el teorema de Morley es cierto.
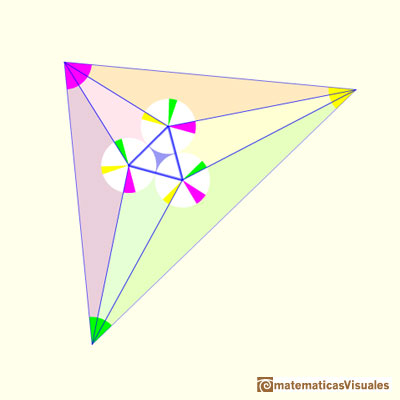
Es decir, el teorema de Morley es verdad para su triángulo y para cualquier triángulo que pudiéramos haber escogido." (John Conway)
REFERENCIAS
 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR
MÁS ENLACES