
La Tierra
Después de estudiar la esfera de Campanus y otros poliedros inscritos en una esfera me ha parecido natural desarrollar un mapa básico de la Tierra en una esfera.

Estudiamos un tipo de poliedros inscritos en una esfera, en particular la llamada esfera de Campanus que fue muy popular durante el Renacimiento y que Luca Pacioli llamó Septuaginta.
A grandes rasgos podemos considerar que la Tierra es una esfera (aunque sabemos que no lo es pues está achatada por los polos, como nos mostró Newton). La Tierra gira alrededor de un eje imaginario que pasa a través de dos puntos de la superficie de la Tierra que llamamos Polo Norte y Polo Sur.
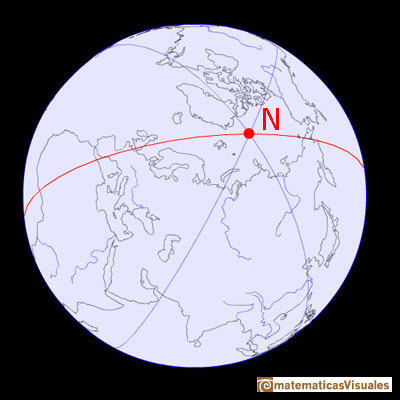
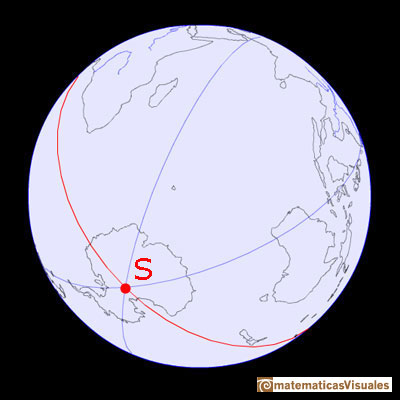
El Ecuador es la intersección entre la Tierra y un plano perpendicular al eje por su punto medio. En el caso de una esfera, sería una circunferencia máxima, es decir, una circunferencia en la esfera que no puede tener el radio mayor.
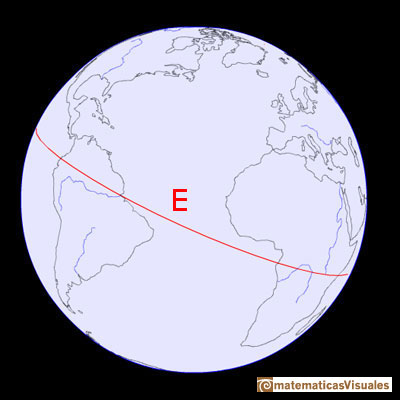
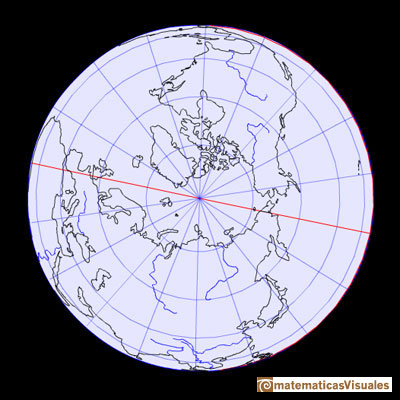
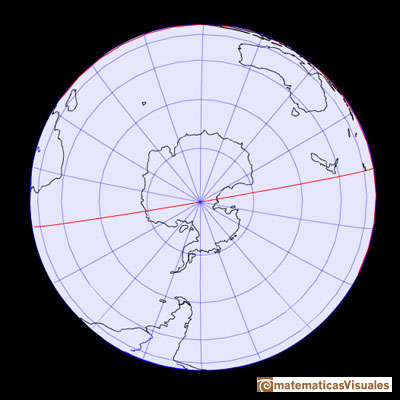
Paralelos al Ecuador se pueden trazar otras circunferencias de latitud. Solemos llamarlos 'paralelos' por esto. Los paralelos son también circunferencias y su radio se hace cada vez más pequeño conforme nos alejamos del Ecuador hacia los polos.
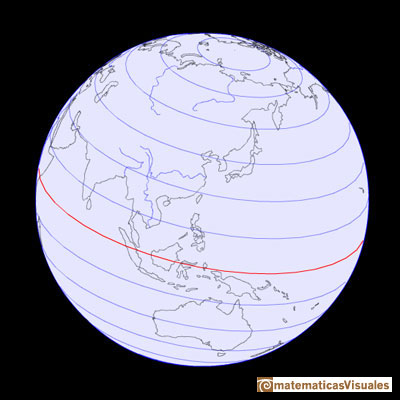
La latitud es una medida de la distancia norte o sur desde el Ecuador. Se suele medir en grados. Al Ecuador se le asigna el valor de 0 grados, al polo Norte está a 90 grados norte y al polo Sur está a 90 grados sur.
Las circunferencias de longitud son circunferencias máximas que pasan a través de los dos polos. Los llamamos 'meridianos'. Estos meridianos son todos iguales mientras que los paralelos tienen uno que es especial, el Ecuador, a partir del cual medimos la latitud.
Para medir la longitud hay que elegir un meridiano. Esta elección es arbitraria y por razones históricas el meridiano 0 es el que pasa por el Real Observatorio en Greenwich, Inglaterra. Lo llamamos meridiano de Greenwich.
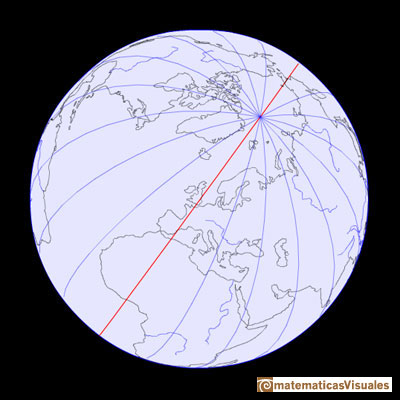
La longitud se mide en grados este u oeste a partir del meridiano de Greenwich.
Resulta interesante destacar que la medida de la latitud es bastante sencilla a partir de observaciones astronómicas conocidas desde la Antigüedad. Sin embargo, conocer la longitud en alta mar es mucho más difícil. Los marinos tuvieron que esperar hasta la invención del cronómetro marino (es decir, un reloj de precisión que mantiene su precisión en un barco) por John Harrison (hacia mediados del XVIII) para poder determinar la posición de un barco en alta mar. Dava Sobel escribió un libro titulado 'Longitude' (hay traducción española) en el que narra las dificultades para determinar la longitud.
Las líneas de latitud y longitud forman una cuadrícula en la esfera. Son un Sistema Geográfico de Coordenadas pues podemos localizar cualquier punto de la Tierra especificando sus dos coordenadas: latitud y longitud.
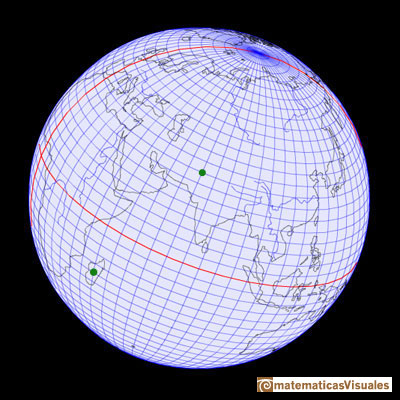
Con la aplicación interactiva de esta página se puede rotar la Tierra y controlar el número de paralelos y meridianos que queremos ver.
REFERENCIAS
Hugo Steinhaus - Mathematical Snapshots - Oxford University Press - Third Edition (p. 197)
Peter R. Cromwell - 'Polyhedra', Cambridge University Press, 1999.
 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR
MÁS ENLACES

Leonardo da Vinci realizó varios dibujos de poliedros para La Divina Proporción de Luca Pacioli. Aquí podemos ver una adaptación del poliedro de 72 caras (Septuaginta) también conocido como esfera de Campanus de Novara.

Cavalieri enunció el teorema que conocemos como Principio de Cavalieri. Usando el Principio de Cavalieri podemos calcular el volumen de una esfera
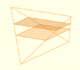
En su artículo 'Two Surprising Theorems on Cavallieri Congruence' (Dos teoremas sorprendentes sobre la congruencia de Cavalieri), Howard Eves describe un tetraedro muy interesante. En esta página calculamos las áreas de sus secciones y su volumen.

El tetraedro de Howard Eves es congruente Cavalieri con una esfera dada. Podemos ver que las secciones correspondientes tienen áreas iguales. Por lo tanto, el volumen de la esfera es el mismo que el volumen del tetraedro. Sabemos calcular el volumen del tetraedro luego ya sabemos el volumen de la esfera (usando una congruencia sorprendente).















